Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 36

Determine os ângulos θ para haver equilíbrio do cilindro de 50 kg e investigue a estabilidade em cada posição. A mola está livre quando θ = 60 º

Passo 1

Desenhando o diagrama do corpo livre

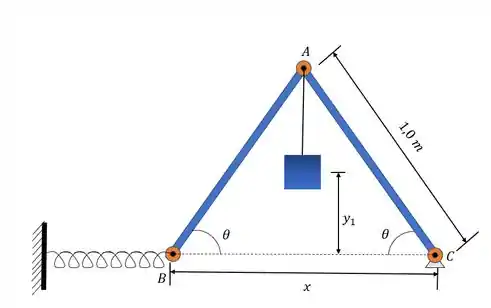
Passo 2

Da geometiria do DLC, temos que:

y 1 = A B ⋅ s e n θ - k = 1,0 ⋅ s e n θ - k

k é a distância do topo da corda até o centro de gravidade da carga:

x = A C ⋅ c o s θ + A B ⋅ c o s θ x = 2 ⋅ c o s θ

Passo 3

O próximo passo é calcular o enlongamento da mola: s = x 60 º - x s = 2 ⋅ c o s 60 º - 2 c o s θ

Passo 4

Calculando as energias potenciais individuais do sistema:Cilindro:

V g = m ⋅ g ⋅ y 1 = 50 × 9,81 × y 1

Mola: V s = 1 2 k × s 2 = 1 2 × 900 × 2 ⋅ 0,5 -     2 c o s θ 2 V s = 1 2 k × s 2 = 450 ( 1 - 4 c o s θ + 4 cos 2 ⁡ θ ) V s = 450 - 1800 c o s θ + 1800 cos 2 ⁡ θ

Passo 5

Podemos agora calcular a energia potencial total do sistema:

V = V g + V s = 50 ⋅ 9,81 ⋅ y 1 = 490,5   s e n θ - k + 450 - 1800 c o s θ + 1800 cos 2 ⁡ θ V = 490,5   s e n θ - k + 450 - 1800 c o s θ + 1800 cos 2 ⁡ θ

Passo 6

Para achar a posição de equilíbrio, precisamos calcular a primeira derivada da expressão:

d V d θ = 490,5 c o s θ + 1800 s e n θ - 3600 ⋅ c o s θ s e n θ

Essa expressão pode ser resolvida por tentativa e erro já que não existe uma formula analítica de se obter a solução. Usando um software computacional: θ = 52,9 º θ = 16,6 º

Passo 7

Para analisar a estabilidade, devemos calcular a expressão da segunda derivada: d 2 V d θ 2 = - 490,5 s e n θ + 1800 c o s θ - 3600 ( - s e n 2 θ + cos 2 ⁡ θ ) d 2 V d θ 2 θ = 52,9 º = - 490,5 s e n 52,9 º + 1800 c o s 52,9 º - 3600 ( - s e n 2 52,9 º + cos 2 ⁡ 52,9 º ) d 2 V d θ 2 θ = 52,9 º = 1675 = > e s t á v e l

d 2 V d θ 2 θ = 16,6 º = - 490,5 s e n 16,6 º + 1800 c o s 16,6 º - 3600 ( - s e n 2 16,6 º + cos 2 ⁡ 16,6 º ) d 2 V d θ 2 θ = 16,6 º = - 1428   > i n s t á v e l

Resposta

θ = 52,9 º = > e s t á v e l θ = 16,6 º = i n s t á v e l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o ângulo θ para haver equilíbrio e investigue a estabilidade nessa posição. As hastes possuem massa de 3k g cada uma e o bloco suspenso D tem massa de 7k g . A corda D C tem comprimento tota
A haste uniforme tem massa de 100k g . Se a mola não estiver deformada quando θ = 60 ° , determine o ângulo θ para haver equilíbrio e investigue a estabilidade na posição de equilíbrio. A mola sempre
O bloco triangular de peso W se apoia sobre os cantos lisos que estão separados por uma distância a . Se o bloco possui três lados iguais de comprimento d , determine o ângulo θ para que haja equilíbr
As duas hastes possuem massa de 8k g cada. Determine a rigidez k exigida para a mola, de modo que haja equilíbrio quando θ = 60 ° . A mola tem comprimento de 1m quando não deformada. Investigue a esta
Determinar o ângulo θ para haver equilíbrio e investigar a estabilidade nessa posição. As hastes possuem massa de 10k g cada e a mola tem comprimento não deformado de 100m m .