Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 21

A viga rígida está apoiada em suas extremidades por dois tirantes de a ç o   A - 36 . Os diâmetros das hastes são d A B   =   12   m m   e   d c d   =   7,5   m m . Se a tensão admissível para o aço for σ a d m   =   115   M P a , determine a intensidade da carga distribuída w e seu comprimento x sobre a viga para que esta permaneça na posição horizontal quando carregada.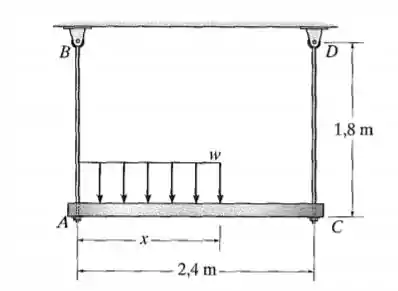

Passo 1

Desejamos encontrar o valor da nossa carga distribuída w e o comprimento x sobre a vida para que a mesma continue na posição horizontal. Dessa forma, precisamos fazer a seguinte interpretação do problema: se queremos que a barra continue na posição horizontal vamos precisar que o alongamento que a haste A B tiver a haste C D deve ter também, ou seja, δ A = δ c . Lembrando que esse alongamento é dado por

δ = F o r ç a   a p l i c a d a ⋅ ( c o m p r i m e n t o   e m   a n á l i s e ) M o d .   d e   e l a s t i c i d a d e ⋅ ( Á r e a   e m   a n á l i s e ) = P L E A

Para nosso caso vamos ter, então, a seguinte construção

δ a = F A b ⋅ L a b E ⋅ A a b   e   δ c = F c d ⋅ L c d E ⋅ A c d

Como essas medidas devem ser iguais podemos fazer

F A b ⋅ L a b E ⋅ A a b = F c d ⋅ L c d E ⋅ A c d   ( i )

Com isso podemos isolar a variável que nos interessar.

Passo 2

Assumindo que ocorra uma falha na haste A B teremos

σ a d m = F a b A a b → F a b = σ a d m ⋅ π 4 ⋅ d 2 ≈ 13,006 k N

Utilizando ( i ) e isolando F c d que é o valor que ainda não temos vamos obter

F c d = d c d d a b 2 ⋅ F a b ≈ 5,081   k N

Passo 3

Das forças internas nas hastes temos

∑ M a = 0 → F c d ⋅ L A c - w ⋅ x ⋅ x 2 = 0

∑ F y = 0 → F c d + F a b - w ⋅ x = 0

Resolvendo esse sistema encontramos w = 13,41 k N m   e   x = 1,35   m . Agora, fazendo essa mesma análise e admitindo falha na haste C D vamos obter

F c d = 5,081 k N   e   F a b = 13,006   k N

Portanto, as duas hastes falham simultaneamente.

Resposta

w = 13,41 k N m   e   x = 1,35 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A coluna de aço A - 36 é usada para suportar as cargas simétricas dos dois pisos de um edifício. Determine o deslocamento vertical de sua extremidade, A , se P 1=200k N ,P 2=310k N e a coluna tiver ár
O eixo de cobre está sujeito às cargas axiais mostradas na figura. Determine o deslocamento da extremidade A em relação à extremidade D se os diâmetros de cada segmento forem d A B=20m m ,d B C=25m me
O conjunto é composto por três hastes de titânio ( T i- 6 A 1 - 4 V ) e uma barra rígida A C . A área da seção transversal de cada haste é dada na figura. Se uma força de 30k N for aplicada ao anel F
O navio é impulsionado na água pelo eixo de uma hélice de aço A - 36 com 8m de comprimento medido desde a hélice até o mancal de encosto D no motor. Se o eixo tiver diâmetro externo de 400m m e espess
A carga é sustentada pelos quatro cabos de aço inoxidável 304 conectados aos elementos rígidos A B e D C . Determine o ângulo de inclinação de cada elemento após a aplicação da carga de 2,5k N . A pos