Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 9
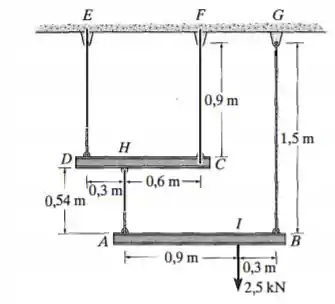
A carga é sustentada pelos quatro cabos de aço inoxidável conectados aos elementos rígidos e . Determine o ângulo de inclinação de cada elemento após a aplicação da carga de . A posição original dos elementos era horizontal e cada cabo tem área de seção transversal de .
Passo 1
Nessa questãonós desejamos encontrar o ângulo de inclinação dos elementos rígidos . Estamos lidando com o aço inoxidável temos que seu módulo de elasticidade é tabelado e dado por . A gente vai precisar encontrar primeiro o descloamento vertical que vai nos ajudar a encontrar o ângulo. A fórmula do deslocamento é.
Bacana, mas a gente não tem os esforços em cada cabo, e aí? Aqui que entra a ideia pra resolver a questão: Vamos separar a estrutura em duas e montar dois diagramas de corpo livre.
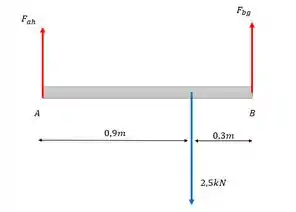
Essa barra vai transferir o esforço invertido para a barra de cima, e o outro DCL vai ficar:
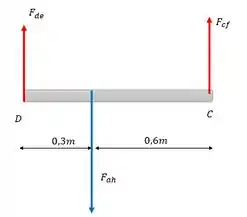
Já aproveitando o gancho bora dá uma anotada nos dados da nossa questão de acordo com a notação que usaremos, assim temos
E ainda da geometria do problema podemos concluir que:
Passo 2
Com o nosso diagrama de corpo livre da barra de baixo, vamos calcular o esforço na barra BG, escolhendo o ponto A para calcular o equilíbrio dos momentos, considerando o sentido horário negativo.
E aí:
Para encontrarmos a força na barra ah, vamos fazer o equilíbrio das forças verticais.
Substituindo a gente tem.
Para a barra mais elevada, também adotando, o sentido anti horário como positivo, vamos usar o segundo diagrama e calcular o somatório dos momentos no ponto D.
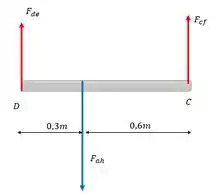
Isolando fcf e substituindo fah, temos:
De forma análoga ao anterior, para as forças verticais nós teremos
Substituindo.
Passo 3
Agora é o momento que você dá uma pausa de uns 15 segundinhos pra dar aquela respirada e voltar pra acabar a questão. Pois bem depois de dar aquela respirada, como agora temos todos os valores das forças podemos calcular o alongamento vertical em , no entanto, vamos descobrir alguns alongamentos antes que servirão de base para esse cálculo. Sendo assim, teremos
O alongamento em vai ser dado por uma combinação de alongamentos, vamos precisar desenhar a barra antes e depois dos deslocamentos pra enxergar melhor.
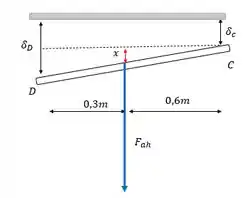
A barra em cinza é na posição inicial, e em branco é após o deslocamento. Pela geometria a gente vê que:
E esse valor x pode ser encontrado por semelhança de triângulos.
Então:
E enfim:
Esse alongamente servirá de base para calcularmos o deslocamento em que será dado por:
Agora, nosso último alongamento que vamos precisar para matar essa questão será o alongamento em dado por
Passo 4
E enfim a gente pode calcular aquele belo ângulo que tanto queríamos, vamos olhar a figura da barra dc deslocada e vamos entender melhor.
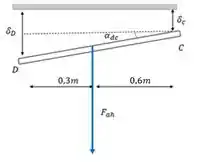
Bacana! Daí tiramos uma relação de tangente que nos dá:
Aplicando a função inversa da tangente em ambos os lados (já que queremos saber só o ângulo) vamos ter
De maneira análoga, vamos encontrar o ângulo para fazendo