Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 4
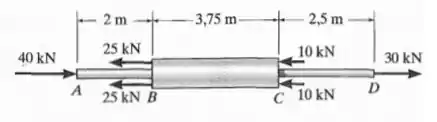
O eixo de cobre está sujeito às cargas axiais mostradas na figura. Determine o deslocamento da extremidade em relação à extremidade se os diâmetros de cada segmento forem . Considere .
Passo 1
Fala queridões, tudo certo com vocês?
Bora pra mais uma resolução marotinha? Vamos (só eu respondo 😕). Antes de tudo, vamos deixar aqui anotado os dados que nós temos e os que podemos inferir a partir do nosso enunciado
Além disso, como o material tratado no problema é o cobre temos que o módulo de elasticidade é tabelado e dado por . Pois bem, qual vai ser o nosso plano de ação para essa questão? Vamos dividir a nosso eixo em três pedaços onde calcularemos o deslocamento da parte e da parte separadamente e, no fim de tudo, o deslocamento de em relação a será dado pela soma desses três valores. Para calcularmos esse deslocamento horizontal vamos usar a seguinte fórmula:
Onde é a extensão do segmento que estamos analisando e a nossa área será dada pela seguinte expressão .
Passo 2
Trabalhando primeiramente com o pedaço do nosso eixo nós teremos
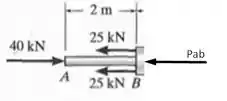
Como nossa barra está em equilíbrio nós teremos que (lembrando que o sinal de negativo se dá por conta do referencial). Assim, utilizando a fórmula dada no passo anterior vamos ter
Agora, vamos pegar para analisar o segmento do nosso eixo cujo esquemático é dado por
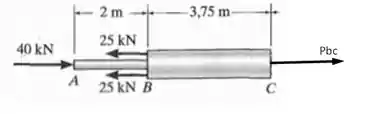
Novamente por conta do equilíbrio nós teremos que e poderemos aplicar a fórmula do passo 1 adequando à esse caso em particular, ficando com
Por fim, vamos analisar o último segmento do nosso eixo que é o dado por
Dessa forma, vamos encontrar e nossa equação do passo 1 terá o seguinte formato
Pronto, agora temos tudo para calcularmos o deslocamento de em relação a basta que façamos a soma de todos os valores encontrados acima e voilà
Acabou o problema sem desespero, deixa o desespero pra quem caiu na trolagem de zoar o coleguinha no instagram.