Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 162

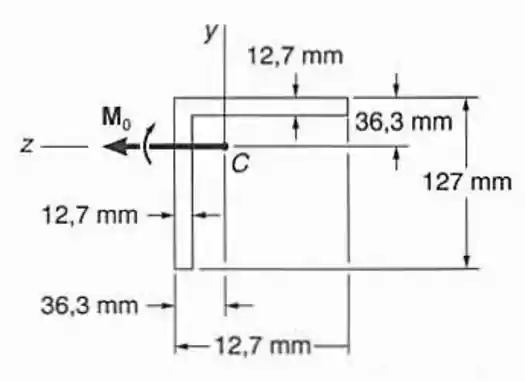
Uma viga com a seção transversal mostrada está sujeita a um momento M 0 que atua em um plano vertical. Determinar o maior valor permissível do momento fletor M 0 , se a máxima tensão na viga não exceder a 80   M P a . Dados: I y = I z = 4,7 × 10 6   m m 4 ; A = 3065   m m 2 ; k m i n = 24,97   m m . (Sugestão: Por razões de simetria, os eixos principais formam um ângulo de 45 ° com os eixos coordenados x e y ; usar também as relações I m i n = A k m i n 2 e I m i n + I m a x = I y + I x ).

Passo 1

Este problema vamos resolver da seguinte maneira:

  • Decompor o momento nas direções principais u e v .
  • Calcular os momentos máximo e mínimo de inércia.
  • Achar o ponto onde a tensão será máxima.
  • Substituir na equação da tensão.

A tensão no ponto será igual a:

σ A = - M v ⋅ u A I v + M u ⋅ v A I u

Passo 2

Achar os momentos nas direções u e v . Como existe a simetria então:

M u = M v = M 0 ⋅ cos ⁡ 45 ° = 0,7071 . M 0

Passo 3

Calcular os momentos máximo e mínimo utilizando a dica dada:

I m i n = A k m i n 2

I m i n = 3065   m m 2 ⋅ ( 24,97   m m ) ²

I m i n = 1,911 × 10 - 6   m 4

I m i n + I m a x = I y + I x

I m a x = I y + I x - I m i n

I m a x = 4,7 × 10 6 + 4,7 × 10 6 - 1,911 × 10 - 6

I m a x = 7,489 × 10 - 6   m 4

Passo 4

O ponto que produzirá a maior tensão será o ponto A:

y A = - 127 - 36,3 = - 90,7   m m

z A = 36,3 - 12,7 = 23,6   m m

Transformando para u A e v A :

u A = y A ⋅ cos ⁡ 45 ° + z A ⋅ s e n ( 45 ° )

u A = - 90,7 ⋅ 0,7071 + 23,6 ⋅ 0,7071

u A = - 47,45   m m

v A = z A ⋅ cos ⁡ 45 ° - y A ⋅ s e n ( 45 ° )

v A = 23,6 ⋅ 0,7071 - ( - 90,7 ) ⋅ 0,7071

v A = 80,82   m m

Passo 5

Agora é só substituir na equação:

σ A = - M v ⋅ u A I v + M u ⋅ v A I u

Lembrando que:

I v = I m i n

I u = I m a x

80   M P a = - 0,7071 . M 0 ⋅ ( 0,04745 ) 7,489 × 10 - 6 + 0,7071 . M 0 ⋅ 0,08082 1,911 × 10 - 6

80 = - 4,48 × 10 - 3 ⋅ M 0 + 30 × 10 - 3 ⋅ M 0

M 0 = 80 25,52 × 10 - 3

M 0 = 3,13   k N ⋅ m

Resposta

M 0 = 3,13   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.