Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 158

Uma carga axial P é aplicada como mostrado a um curto perfil laminado de aço W 200 × 35,9 . Determinar a maior distância a , para que a máxima tensão de compressão não exceda a 1125   M P a .

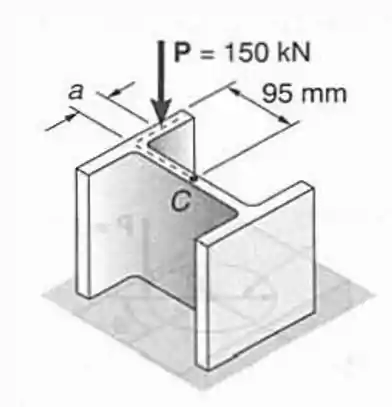
Passo 1

A tensão no ponto será igual a:

σ A = - P A - M z ⋅ y A I z + M y ⋅ z A I y

Logo, para resolver este problema basta achar a área, os momentos decompostos em x e y , assim como os momentos de inércia também decompostos. Vamos lá!?

Passo 2

Primeiro vamos lá na tabela do final do livro para achar os momentos de inércia e a área:

I y = 7,62 × 10 6   m m 4 = 7,62 × 10 - 6   m 4

I z = 34,5 × 10 6   m m 4 = 34,5 × 10 - 6   m 4

A = 4570   m m 2 = 4,57 × 10 - 3   m 2

Passo 3

A força P vai gerar dois momentos, um em z e outro em y da forma:

M y = - ( P ⋅ a )   N ⋅ m

M z = - 150000 ⋅ 0,095 = - 14250   N ⋅ m

Passo 4

Agora é só substituir na equação:

σ A = - P A - M z ⋅ y A I z + M y ⋅ z A I y

Vamos utilizar z a como metade do comprimento da aba do nosso perfil z a = 165 / 2     m m e no lugar de y a vamos utilizar a altura da aba y a = - 201 / 2     m m

- 1125   M P a = - 150000 4,57 × 10 - 3 - - 14250 ⋅ ( - 0,1005 ) 34,5 × 10 - 6 + M y ⋅ ( 0,0825 ) 7,62 × 10 - 6

- 1125 = - 32,82 - 41,51 + 0,0108 ⋅ M y

M y = - 1125 + 32,82 + 41,51 0,0108 = - 97284,8   N ⋅ m

Como

M y = - ( P ⋅ a )   N ⋅ m

- 97284,8   = - ( P ⋅ a )  

a = 97284,8   150000 = 65   m m

Resposta

a = 65   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o P r o b l e m a4.121 considerando que as deformações medidas são: ε A = + 600μ eε B = + 420μ
Uma coluna curta em perfil laminada de aço suporta uma placa rígida na qual duas ações PeQ são aplicadas conforme mostrado. As deformações foram medidas nos dois pontos AeB na linha de centro da face
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
Uma única força vertical P é aplicada a um poste curto de aço conforme mostrado. Extensômetro localizados em A, B e C indicam as seguintes deformações: ε A = - 500μ eε B = - 1000μ eε C = - 200μ Sabend