A viga uniforme de é suportada pela corda que está presa à sua extremidade, contorna o pino áspero e depois conecta-se ao bloco de . Se o coeficiente de atrito estático entre a viga e o bloco, e entre a corda e o pino, for , determine a distância máxima a que o bloco poderá ser colocado a partir de A e ainda permanecer em equilíbrio. Considere que o bloco não tombará.
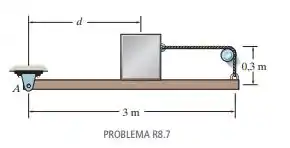
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Partiu mais uma questão de Resmat.
Primeiramente, devemos calcular a força que o peso do conjunto gera:
Esta força é transmitida para o cabo e puxa o bloco. O que sustenta isso é a força de atrito. Ela é dada pelo peso do bloco vezes o coeficiente de atrito:
Como podemos ver, o bloco deslizar não depende da distância.
Resposta
A distância do bloco não influencia.