Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 87
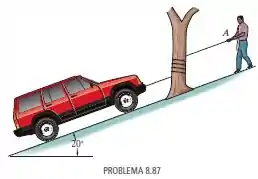
O veículo, que tem massa de , deve descer a rampa com velocidade constante, sendo para isso sustentado pela corda enrolada na árvore e mantida esticada pelo homem. Se as rodas estão livres para girar e o homem em pode resistir a um puxão de , determine o menor número de voltas ao redor da árvore necessário para que isso ocorra. O coeficiente de atrito cinético entre a árvore e a corda é .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Sabemos que o ângulo de fricção é dado por:
Portanto:
O ângulo de avanço do parafuso é dado por:
Substituindo os dados, temos que:
Passo 2
Agora vamos calcular o menor torque necessário para afrouxar o parafuso. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
Determine o intervalo de valores de P para o qual o equilíbrio do bloco mostrado na figura é mantido.
Considerando apenas valores de θ menores que 90°, determine o menor valor de θ solicitado para o qual o movimento do bloco para a direita é iminente quando ( a ) W = 340 N, ( b ) W = 450 N.
Os coeficientes de atrito entre o bloco e o trilho são μ s = 0,3 e μ k = 0,25 . Sabendo que θ = 65 ° , determine o menor valor da força P necessária ( a ) para iniciar o movimento do bloco sobre o tri
O bloco de 360 N está ligado à articulação AB e repousa sobre uma esteira em movimento. Sabendo que μ s = 0,25 e μ k = 0,2 determine a intensidade da força horizontal P que pode ser aplicada na esteir
Três pacotes de 4 kg, A, B e C são colocados em uma esteira transportadora que está em repouso. Entre a esteira e os pacotes A e C, os coeficientes de atrito são μ s = 0,3 e μ k = 0,2 ; entre o pacote