Foram coletadas observações da variável , representando o número de vestibulares prestados por um aluno até passar. A tabela de frequência para é a seguinte:
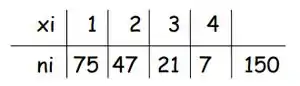
Calcule as medidas de posição da variável e da variável despesa com o vestibular definida como , onde é o custo com a inscrição por vestibular e o custo com a preparação para o vestibular, assumido ser realizado uma única vez.
Passo 1
Medidas de posição são as médias, medianas e modas dos dados.
Começando por , a média vai ser dada pela média aritmética. No nosso caso temos dados numa tabela de freqüência, então nossa média aritmética é calculada por:
A mediana vai ser o valor central, mas não vamos precisar escrever todos os valores em ordem para ver quem tá no meio, repara comigo... temos dados, então os centrais vão estar nas posições e , certo? Se ficar com dúvida, testa pra um número pequeno, tipo :
Os valores centrais são e , concorda?
Beleza, então sabendo quem são as posições dos valores centrais, vamos na tabela de frequência descobrir o valor desses caras. Repara que aparece vezes, então a posição é . E a posição vai ser a imediatamente após a , certo? Que é quando . Então nossa mediana vai ser a média entre esses dois valores:
E para a moda... é só ver qual tem maior frequência, que é o . Então:
Passo 2
Para calcular os valores de , basta substituirmos os que existem na equação:
Então:
Para calcular a média, vamos usar a mesma fórmula que usamos com a frequência relativa (que é a mesma frequência do que usamos na equação de cada ):
A agora a posição é ocupada por e a posição por , então a mediana é:
E a moda é o valor com mais frequência, o relacionado ao , que é o de maior freqüência, ou seja, :