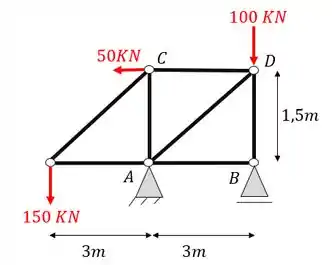
Determine o normal da barra AB e CD da treliça abaixo, usando o método da seção de Richter.
Passo 1
Para resolvermos a nossa treliça pelo método da seção de Richter precisamos ter me mente o seguinte passo a passo.
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que temos que fazer é passar uma seção que corte a barra que pretendemos calcular, e que além disso respeite a regrinha de cortar apenas 3 barras.
- A terceira coisa que devemos fazer é eliminar um dos lados da treliça quando tivermos definido a seção de Richter.
- A quarta coisa que devemos fazer é o equilíbrio da seção que nos restar. Nesse equilíbrio iremos calcular os normais das barras que tivermos cortado.
- Por fim, o quinto e último passo consiste em escolher a melhor forma de fazer o equilíbrio das seções. Na grande maioria das vezes a melhor atitude a se tomar é calcular o somatório de momentos em um nó que receba duas barras da nossa seção cortada, pois pense bem, se cortamos 3 barras e vamos fazer o somatório de momentos em um nó que recebe 2 barras, no nosso problema teremos apenas 1 incógnita, e assim essa incógnita será exatamente o normal de um das barras.
As reações

E as equações de equilíbrio
Entendido o nosso passo a passo, vamos usá-lo no nosso exercício.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
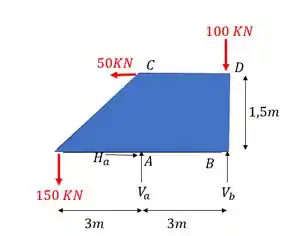
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
Como deu negativo, sabemos que só significa que a direção do vetor que escolhemos está equivocada, ou seja, basta mudarmos a direção do vetor para ficarmos com a direção correta e assim podermos usar o sinal positivo ao invés do negativo
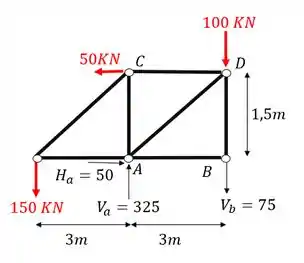
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
A segunda parte do problema consiste em cortar as barras que queremos calcular os normais, lembrando de respeitar a regra das 3 barras. Se der para cortar todas que queremos calcular de uma só vez, podemos fazer isso, se não, vale apena fazer uma de cada vez, caso não seja possível cortar tudo com uma única seção de Richter. No nosso exercício, conseguimos fazer isso, cortar 3 barras, e das 3 que cortamos, duas são as que precisamos calcular, em baixo temos a nossa seção
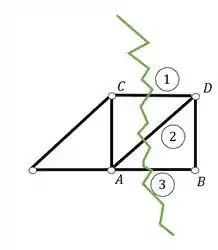
Passo 4
O quarto passo consiste em escolher um dos lados da seção para permanecer e descartar o outro lado da seção. Se pararmos para olhar a nossa seção com os carregamentos
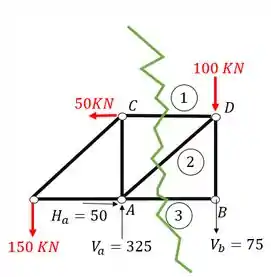
Podemos ver que a parte da treliça a esquerda da seção de Richter possui muito mais carregamentos do que a seção do lado direito, logo, para ficar mais fácil de calcular, iremos descartar o lado esquerdo, e permaneceremos com o lado direito, com isso a nossa seção passa a ser
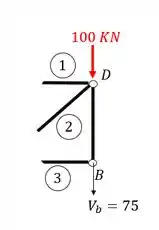
E sabemos que devemos, para toda barra cortada, colocar um normal saindo da seção que foi cortada, o que simboliza exatamente o quarto passo do nosso passo a passo.
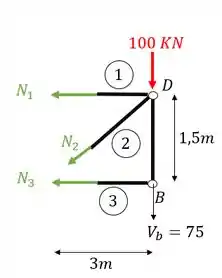
Passo 5
Agora o quinto e último passo consiste em escolhermos a melhor opção para fazermos o equilíbrio dos normais.
Veja que por exemplo, se quisermos calcular o normal 1, precisamos fazer o equilíbrio de momentos fletores no nó A, que mesmo sendo descartado por estar na parte esquerda da treliça, sabemos o seu posicionamento, e por isso podemos fazer o somatório de momentos nele.
Mas você pode se perguntar, porque o nó A?
Veja que as barras AD e AB se encontram no ponto A, e além disso, são incógnitas, ou seja, se fizermos o somatória de momentos no nó A, que sabemos que tem que ser igual a zero por ser um treliça, teremos que a única incógnita do problema será que queremos calcular, fazendo isso teremos
Viu como é simples? Com 3 linhas já achamos o valor do normal .
Porém também é pedido no enunciado o normal da barra 3, ou seja, , vamos lá então.
Passo 6
Agora qual seria a melhor opção para calcularmos o ?
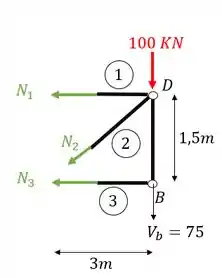
Vemos que nesse caso a melhor opção seria fazer o somatório de momentos no nó D, pois veja que as barras 1 e 2 são incógnitas (fingindo que anda não temos o normal 1), e ambas as barras chegam no nó D, ou seja, quando fizermos essa conta a única incógnita que restará será o , vamos lá então.
Ou seja, mais 3 linhas calculamos o segundo normal, e veja que a barra 1 representa a barra CD, e a barra 3 representa a barra AB, que são as pedidas no enunciado, dessa forma podemos escrever os normais como.