Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método de Ponchon – Savarit – Colunas Especiais

Ver Teoria
Exercício 71234568

Enunciado

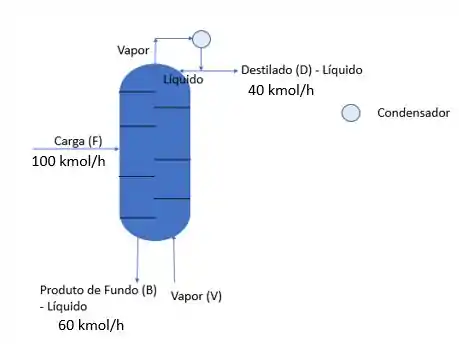
Faça o balanço de energia da coluna de vapor de arraste abaixo e encontre o valor de V n + 1 considerando desprezível a troca de calor. Dados: h f = 30   k m o l / h , H n + 1 = 15 k m o l / h   e   h d = h b = 45 k m o l / h .      

Passo 1

Primeira que coisa que vamos fazer aqui é o balanço energético dessa coluna, ou seja:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Então vamos escrever essa expressão em termos genéricos para depois substituir os valores, beleza?

Passo 2

O balanço de energia na coluna vai ficar:

F ∙ h f + V n + 1 ∙ H n + 1 - D ∙ h d - B ∙ h b = q c

Lembrando que   q c D = Q c , porém, o enunciado nos disse para considerar desprezível a troca de calor, então:

Q c = q c = 0

Logo,

F ∙ h f + V n + 1 ∙ H n + 1 - D ∙ h d - B ∙ h b = 0

Passo 3

Porém, queremos encontrar V n + 1 ,   então, vamos reorganizar a expressão anterior:

V n + 1 ∙ H n + 1 = D ∙ h d + B ∙ h b - F ∙ h f

V n + 1 = D ∙ h d + B ∙ h b - F ∙ h f H n + 1

Substituindo os valores,

V n + 1 = 40 ∙ 45 + 60 ∙ 45 - 100 ∙ 30 15

E fazendo as contas temos que,

V n + 1 = 100   k m o l / h

Resposta

V n + 1 = 100   k m o l / h