Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Método de Ponchon – Savarit – Colunas Especiais

Ver Todos os Exercícios

Teoria

Importância desse tópico

Até agora vimos como aplicar o método de Ponchon Savarit para determinar número de estágios, razão de refluxo e alguns outros parâmetros de coluna de destilação. Agora, nós vamos avaliar mais alguns casos de coluna para facilitar a metodologia de dedução, beleza? As colunas que veremos serão coluna de vapor de arraste, coluna de retificação e coluna de esgotamento.

No entanto, o procedimento será o mesmo que vimos nos tópicos anteriores. Portanto, neste tópico vamos apenas entender como aplica o balanço de energia nesses casos e como marcar os pontos no gráfico, beleza? Para ver a aplicação em um problema completo, bora lá para os exercícios.

Método Ponchon – Savarit com colunas de vapor de arraste

Podemos começar desenhando a nossa coluna de vapor de arraste. E podemos traçar uma envoltória nessa coluna.

O balanço de energia na coluna vai ficar:

F ∙ h f + V n + 1 ∙ H n + 1 = D ∙ h d + q c + B ∙ h b

Reorganizando, lembrando que   q c D = Q c , obtemos que:

F ∙ h f = D ∙ h d + Q c + B ∙ h b - V n + 1 ∙ H n + 1

Podemos definir um ponto ∆ B - = B ∙ h b - V n + 1 ∙ H n + 1 . Com isso, substituindo esse ponto na expressão anterior, a equação fica bem mais simples com 3 pontos colineares e também considerando que D h d + Q c = ∆ D .

F ∙ h f = ∆ D + ∆ B -

Portanto, podemos traçar os pontos colineares que identificamos pelas equações para achar a interseção ∆ B - .

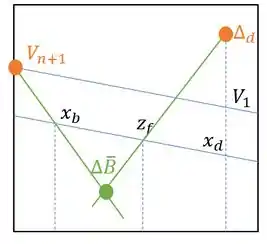
Método Ponchon – Savarit com colunas de Retificação

As colunas de retificação são aquelas que não possuem refervedor e não possuem coluna de esgotamento. Com isso, a carga entra por baixo como vapor. A representação dessa coluna é dada por:

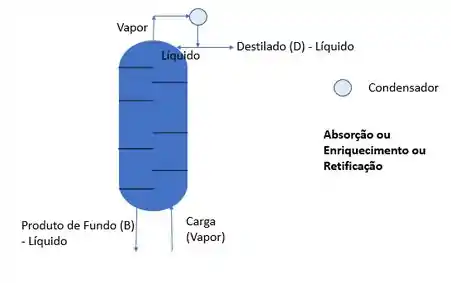
Com isso, o balanço de energia dessa coluna fica:

F ∙ H f = B ∙ h b + D . h d + q c

Reorganizando, temos que:

F ∙ h f = D ∙ h d + Q c + B ∙ h b

E, marcando os pontos colineares, o gráfico fica com essa carinha aqui:

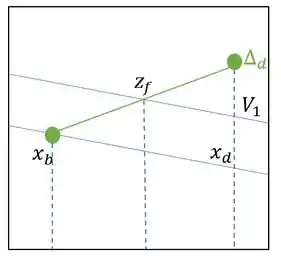
Método Ponchon – Savarit com colunas de Esgotamento

As colunas de esgotamento, por sua vez, não possuem a seção de absorção e também não possuem condensador. Portanto, a carga entra líquida pelo topo.

O balanço de energia nessa coluna será dado por:

F ∙ h f + q r = B ∙ h b + V 1 ∙ H 1

E se novamente reorganizarmos a nossa equação, obteremos que os pontos colineares são dados por:

F ∙ h f = V 1 ∙ H 1 + ∆ B

E marcando esses pontos no gráfico, a reta vai ficar mais ou menos com esse perfil:

Portanto, a gente viu os principais tipos de coluna que podem aparecer 😊 Corre lá para os exercícios para vermos como aplicar isso tudo!

Método Ponchon – Savarit com colunas de Retificação

Método Ponchon – Savarit com colunas de Esgotamento

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Cite três exemplos de colunas especiais.

Passo 1

As colunas especiais não são tão comuns de aparecer nas questões de prova mas é bom conhecermos.

Passo 2

Alguns exemplos de colunas especiais são: coluna de vapor de arraste, coluna de retificação e coluna de esgotamento.

Resposta

Coluna de vapor de arraste, coluna de retificação e coluna de esgotamento.

Exercício Resolvido #2

Elaboração própria

Faça um desenho esquemático da coluna de retificação e da coluna de esgotamento.

Passo 1

As colunas de retificação são aquelas que não possuem refervedor e não possuem coluna de esgotamento. Com isso, a carga entra por baixo como vapor, esquematicamente temos:

Passo 2

Já a coluna de não possuem a seção de absorção e também não possuem condensador. Portanto, a carga entra líquida pelo topo. Esquematicamente:

Resposta

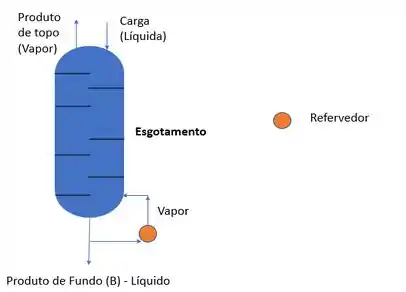
Exercício Resolvido #3

Elaboração própria

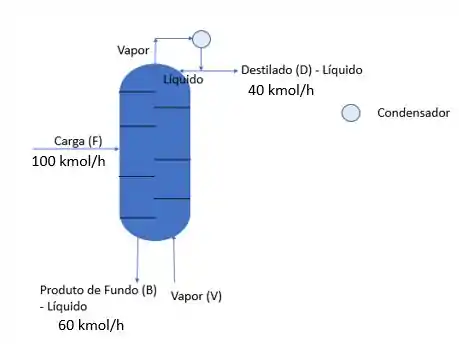
Faça o balanço de energia da coluna de vapor de arraste abaixo e encontre o valor de V n + 1 considerando desprezível a troca de calor. Dados: h f = 30   k m o l / h , H n + 1 = 15 k m o l / h   e   h d = h b = 45 k m o l / h .      

Passo 1

Primeira que coisa que vamos fazer aqui é o balanço energético dessa coluna, ou seja:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Então vamos escrever essa expressão em termos genéricos para depois substituir os valores, beleza?

Passo 2

O balanço de energia na coluna vai ficar:

F ∙ h f + V n + 1 ∙ H n + 1 - D ∙ h d - B ∙ h b = q c

Lembrando que   q c D = Q c , porém, o enunciado nos disse para considerar desprezível a troca de calor, então:

Q c = q c = 0

Logo,

F ∙ h f + V n + 1 ∙ H n + 1 - D ∙ h d - B ∙ h b = 0

Passo 3

Porém, queremos encontrar V n + 1 ,   então, vamos reorganizar a expressão anterior:

V n + 1 ∙ H n + 1 = D ∙ h d + B ∙ h b - F ∙ h f

V n + 1 = D ∙ h d + B ∙ h b - F ∙ h f H n + 1

Substituindo os valores,

V n + 1 = 40 ∙ 45 + 60 ∙ 45 - 100 ∙ 30 15

E fazendo as contas temos que,

V n + 1 = 100   k m o l / h

Resposta

V n + 1 = 100   k m o l / h

Exercício Resolvido #4

Elaboração própria

Faça o balanço de energia da coluna de retificação abaixo e encontre o valor de H f   considerando desprezível a troca de calor. Dados:     h d = h b = 45 k m o l / h   .    

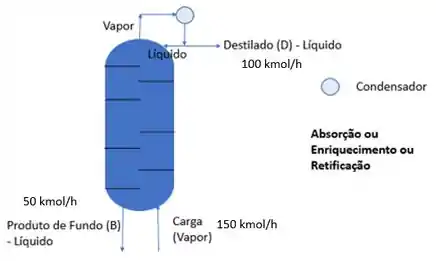
Passo 1

Primeira que coisa que vamos fazer aqui é o balanço energético dessa coluna, ou seja:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Então vamos escrever essa expressão em termos genéricos para depois substituir os valores, beleza?

Passo 2

Com isso, o balanço de energia dessa coluna fica:

F ∙ H f - B ∙ h b - D . h d = q c

Lembrando que   q c D = Q c , porém, o enunciado nos disse para considerar desprezível a troca de calor, então:

Q c = q c = 0

Logo,

F ∙ H f - B ∙ h b - D . h d = 0

Passo 3

Porém, queremos encontrar H f ,   então, vamos reorganizar a expressão anterior:

F ∙ H f = B ∙ h b + D . h d

H f = B ∙ h b + D . h d F

Substituindo os valores,

H f = 5 0 ∙ 45 + 10 0 ∙ 45 15 0

E fazendo as contas temos que,

H f = 45   k m o l / h

Resposta

H f = 45   k m o l / h

Exercício Resolvido #5

Elaboração própria

Faça o balanço de energia da coluna de esgotamento abaixo e encontre o valor de V 1   considerando desprezível a troca de calor. Dados:   h f = 1 0   k m o l / h , H 1 = 5 7   k m o l / h     e   h b = 1 5 k m o l / h .      

.    

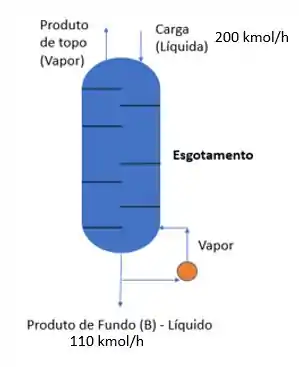
Passo 1

Primeira que coisa que vamos fazer aqui é o balanço energético dessa coluna, ou seja:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Então vamos escrever essa expressão em termos genéricos para depois substituir os valores, beleza?

Passo 2

Com isso, o balanço de energia dessa coluna fica:

F ∙ h f - B ∙ h b - V 1 ∙ H 1 = q r

Lembrando que   q c D = Q c , porém, o enunciado nos disse para considerar desprezível a troca de calor, então:

Q c = q c = 0

Logo,

F ∙ h f - B ∙ h b - V 1 ∙ H 1 = 0

Passo 3

Porém, queremos encontrar H f ,   então, vamos reorganizar a expressão anterior:

V 1 ∙ H 1 = F ∙ h f - B ∙ h b

V 1 = F ∙ h f - B ∙ h b H 1

Substituindo os valores,

V 1 = 20 0 ∙ 10 + 1 1 0 ∙ 1 5 57

E fazendo as contas temos que,

V 1 = 64   k m o l / h

Resposta

V 1 = 64   k m o l / h

Exercício Resolvido #6

Elaboração própria

A partir do gráfico da coluna de vapor de arraste abaixo encontre ∆ B - .

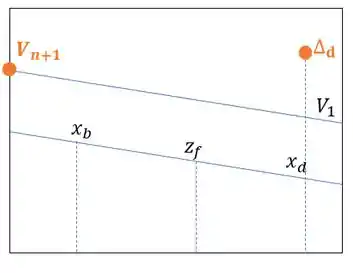
Passo 1

Podemos encontrar a interseção ∆ B -   traçando os pontos colineares. Então, vamos unir os pontos.

Passo 2

Primeiro vamos traçar uma reta passando pelos pontos V n + 1 e x b , da seguinte forma:

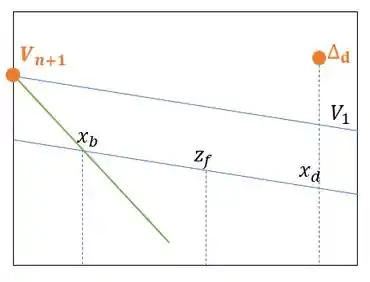
Passo 3

Agora podemos traçar outra reta passando pelos pontos ∆ d e z f , da seguinte forma:

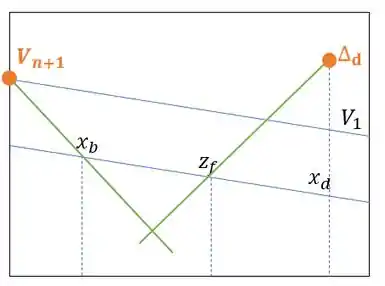
E esse ponto de interseção entre as duas retas que traçamos vai ser o nosso ∆ B - .

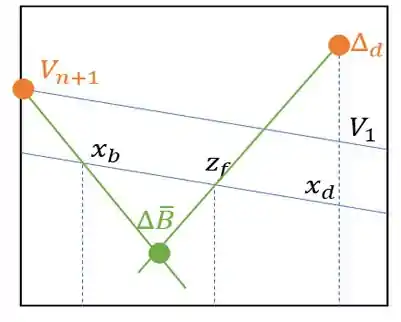
Feshow! \o/

Resposta

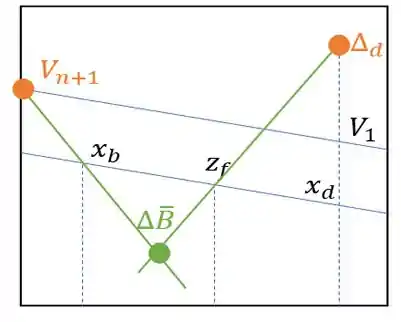
Exercício Resolvido #7

Elaboração própria

Calcule o número de estágios da coluna de retificação cujo sistema se encontra descrito por:

Passo 1

Antes de dar início ao nosso procedimento de Ponchon Savarit para encontrar o número de estágios necessários. Precisamos, encontrar a nossa reta de operação. Então bora ver como isso vai ficar!

Passo 2

Nós podemos encontrar a nossa reta de operação unindo os pontos x b e ∆ d . Com isso, encontramos, também, z f .

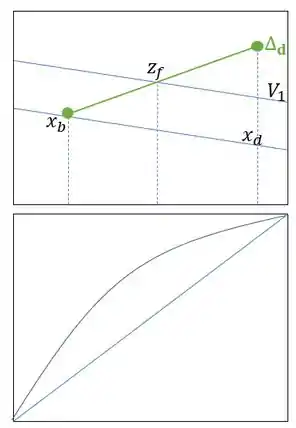
Passo 3

Com a nossa reta de operação pronta, podemos dar início ao procedimento de Ponchon Savarit seguindo os passos abaixo, como já vimos antes.

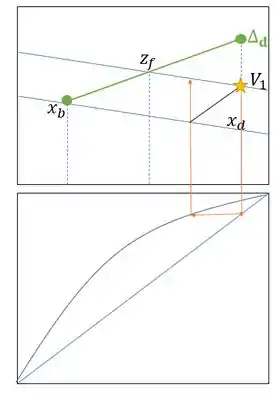
Passo 4

Após seguir o procedimento de Ponchon Savarit obtemos um total de 3 estágios.

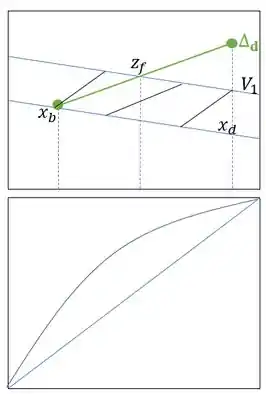
Resposta

3 estágios.

Exercício Resolvido #8

Elaboração própria

Calcule o número de estágios da coluna de esgotamento cujo sistema se encontra descrito por:

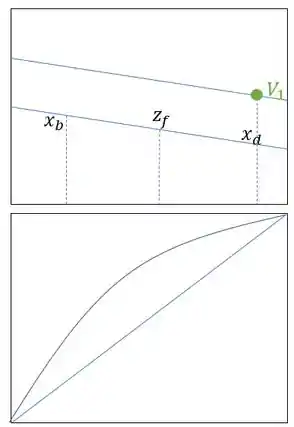
Passo 1

Antes de dar início ao nosso procedimento de Ponchon Savarit para encontrar o número de estágios necessários. Precisamos, encontrar a nossa reta de operação. Então bora ver como isso vai ficar!

Passo 2

Nós podemos encontrar a nossa reta de operação unindo os pontos V 1 e z f . Prolongando essa reta, podemos encontrar ∆ B   da seguinte forma:

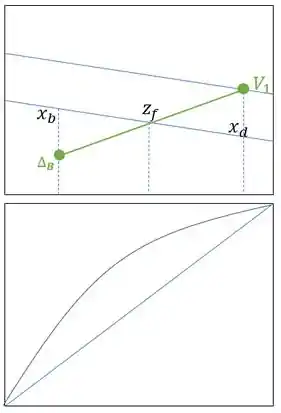
Passo 3

Com a nossa reta de operação pronta, podemos utilizar o procedimento de Ponchon Savarit, que já vimos antes, resultando em 3 estágios.

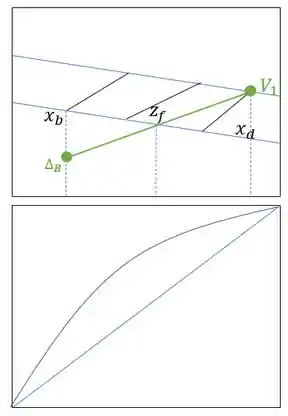
Resposta

3 estágios.