Uma mistura binária contendo molar da espécie mais volátil é alimentada, em seu ponto de bolha, a uma coluna de pratos que opera à pressão atmosférica. Deseja-se que a fração molar da espécie mais volátil seja molar no destilado e de molar no resíduo. A coluna utiliza um condensador parcial com retirada de vapor e um refervedor parcial. Utilizando o método de Ponchon-Savarit e o diagrama entalpia-composição fornecidos para o sistema, determine o valor da razão de refluxo mínima.
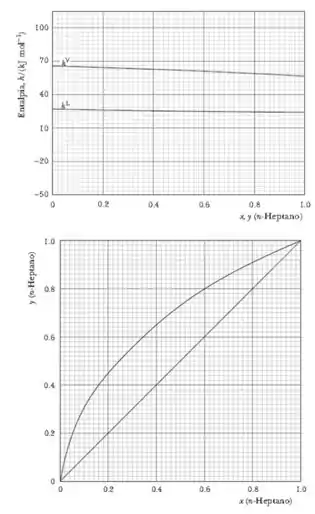
Passo 1
A questão nos forneceu o gráfico do diagrama xy e o gráfico do diagrama de fases. E nos é pedido para calcular a Razão de Refluxo mínima que já sabemos que tem a seguinte fórmula:
Então, precisamos descobrir os valores dos elementos da equação.
Passo 2
A partir do , fornecido pela questão, conseguimos encontrar o valor de pelo diagrama xy, pois o e o estão em equilíbrio. Assim, encontramos
Para na curva de líquido saturado, , para na curva de vapor saturado, . E para , pelo diagrama xy.
Interligando os pontos e por uma reta, obtém-se que em
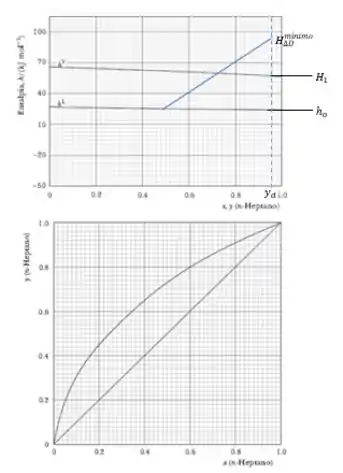
Passo 3
Agora que já encontramos todos os dados necessários, podemos jogar na fórmula.