Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Método de Ponchon – Savarit – Razão de Refluxo

Ver Todos os Exercícios

Teoria

Importância

Pessssoooal, bora entender como calcular a Razão de Refluxo no método Ponchon Savarit?!?

Só que lembra que a gente viu que tem mais de uma Razão de Refluxo, temos a operacional, a mínima e a total. Vamos ver caso a caso ok?

Razão de Refluxo Operacional

Podemos escrever a Razão de Refluxo Operacional a partir dessa fórmula aqui:

R R = L o D = H ∆ D - H 1 H 1 - h o

E se te pedirem a Razão de Refluxo Interna, pode usar essa fórmula aqui:

R R i n t e r n a = L o V 1 = H ∆ D - H 1 H ∆ D - h o

E vou colocar aqui uma representação simplificada de como retirar esses valores do gráfico, ok? Para isso, vamos usar um gráfico em que todos os estágios já foram determinados, conforme aquele procedimento que vimos, beleza?

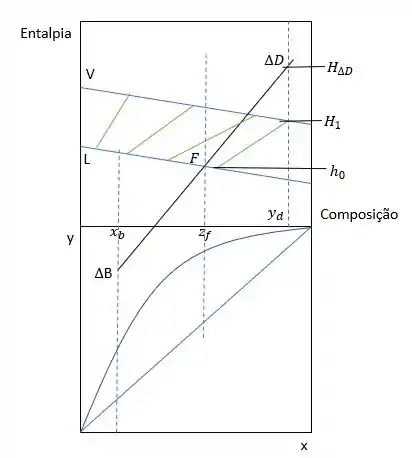
E, se por acaso, o condensador fosse total ao invés de parcial, a representação dos pontos que precisamos ficaria desse jeitinho aqui:

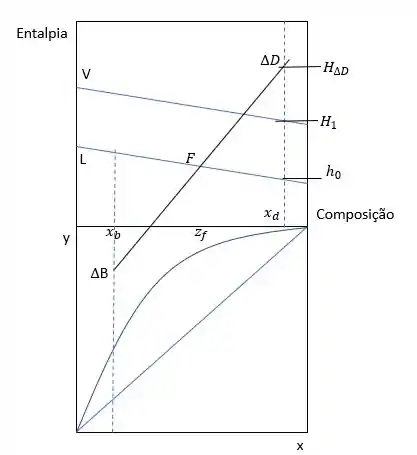
Assim, em condensador total, ficam todos os pontos na mesma direção já que o líquido que é o produto de topo ( D ), o líquido que volta para o coluna e o vapor que passa pelo condensador possuem a mesma composição.

Razão de Refluxo Mínima

Para calcular a Razão de Refluxo mínima, a fórmula que devemos usar é a mesma. No entanto, a forma que pegamos no gráfico o ponto do condensador vai mudar. Para pegar esse ponto, vai ser necessário determinar a Linha de amarração que passa pelo ponto de carga e estender essa linha para determinar o H ∆ D m í n i m o , vou mostrar graficamente para ficar mais simples, ok?

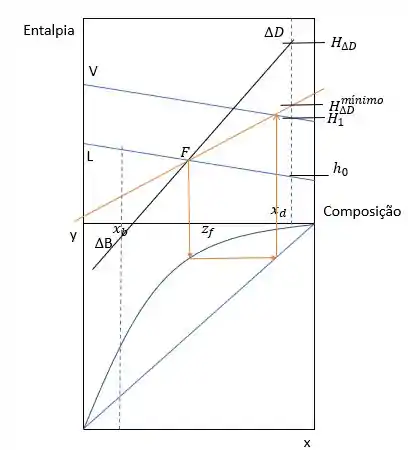
Então, precisamos deixar o x e y da carga em equilíbrio. Traçar uma reta entre eles e estender até a vertical x d . Nessa vertical, vamos achar o H ∆ D m í n i m o . E aí a fórmula fica assim:

R R = L o D = H ∆ D m í n i m o - H 1 H 1 - h o

Razão de Refluxo Total

Lembrando do que aprendemos de Razão de Refluxo total, ela ocorre quando nada do produto sai como produto de topo ou fundo, ou seja, tudo que sai do nosso condensador ( que foi o vapor condensado) volta para a coluna de destilação. Como vamos determinar o número de estágios quando tivermos nessa condição?

Nesse caso, vamos considerar que as retas de operação são verticais, pois é como se elas tivessem indo para o infinito, então traçando os estágios na Razão de Refluxo Total, obtemos algo parecido com isso:

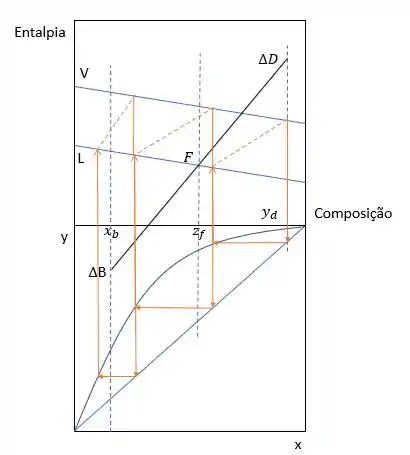
Logo, o nosso número mínimo de estágios são 3, que são os pontilhadinhos laranja, beleza?

Razão de Refluxo Mínima

Razão de Refluxo Total

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

O que ter uma Razão de Refluxo total implica graficamente?

Passo 1

A Razão de Refluxo total ocorre quando tudo que sai do nosso condensador ( que foi o vapor condensado) volta para a coluna de destilação. Ai para determinar o número de estágios vamos considerar que as retas de operação são verticais, pois é como se elas estivessem indo para o infinito.

Resposta

Graficamente, vamos considerar que as retas de operação são verticais.

Exercício Resolvido #2

Elaboração própria

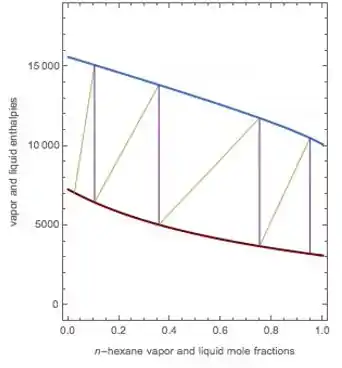
Considerando um sistema que temos Razão de Refluxo total representado pelo diagrama abaixo. Indique a(s) reta(s) de operação e o número de estágios.

Passo 1

Repara que para o caso de refluxo total, a representação gráfica é diferente das demais. Aqui, nós vamos ter quatro retas de operação representadas pelas retas verticais (roxas) no diagrama.

Passo 2

Beleza, mas e o número de estágio? Esse vamos raciocinar da mesma forma que para os outros casos. Onde os estágios são representados pelas retas diagonais (verdes). Assim, temos um total de quatro estágios.

Resposta

Retas de operação: retas verticais (roxas)

Número de estágios: 4

Exercício Resolvido #3

Elaboração própria

Calcule a Razão de Refluxo Operacional pelo método Ponchon-Savarit sabendo que x d = 0,86 .

Passo 1

A questão nos deu um gráfico em que todos os estágios já foram determinados, conforme o procedimento que vimos antes. E nos pede para calcular, a Razão de Refluxo Operacional que sabemos que tem a seguinte fórmula:

R R = L o D = H ∆ D - H 1 H 1 - h o

Então, precisamos encontrar os elementos no gráfico para calcular nossa R R .

Passo 2

Precisamos encontrar no gráfico os valores de H ∆ D ,     H 1   e   h o . Conseguimos encontrar o valor de H 1 a partir do encontro do primeiro estágio (primeira reta roxa da direita para a esquerda) com a curva de vapor (curva azul).

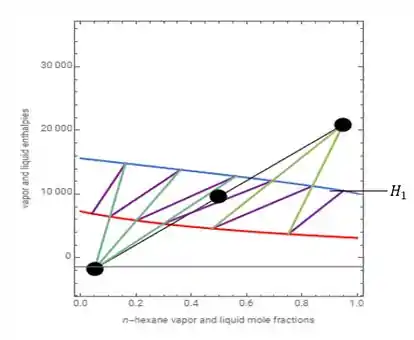
Assim, vemos que H 1 = 1 05 00   K J / m o l , lembrando que por ser uma leitura gráfica os valores podem não ser tão certinhos mas encontrando algo próximo a isso está ótimo!

Passo 3

Em seguida, conseguimos encontrar o valor de h o a partir do encontro do primeiro estágio (primeira reta roxa da direita para a esquerda) com a curva de líquido (curva vermelha).

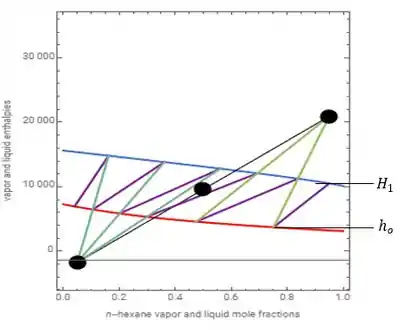
Assim, vemos que h o = 3 950   K J / m o l

Passo 4

Para encontrar o valor de H ∆ D , precisamos primeiro marcar o valor de x d = 0,86 no gráfico.

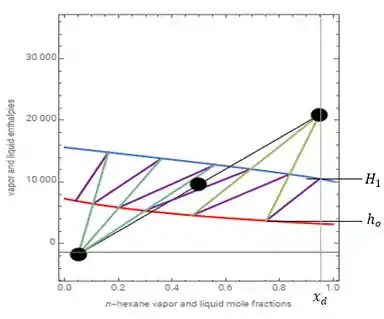
Repara que traçamos uma reta vertical (em cinza claro) para facilitar na hora de encontrarmos o que queremos, beleza?

Agora, nós vamos ter que o encontro dessa nossa nova reta com a reta de operação (em preto), que vai ser o valor do nosso H ∆ D = 20600   K J / m o l .

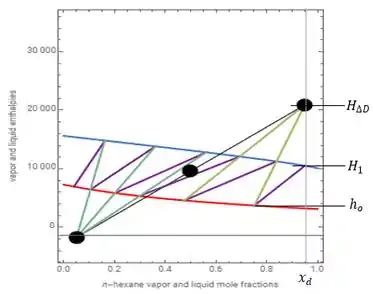
Passo 5

Agora que já encontramos todos os nossos elementos no gráfico, podemos (finalmente), calcular o valor da Razão de Refluxo Operacional.

R R = H ∆ D - H 1 H 1 - h o = 20600 - 10500 10500 - 3950

R R = 1,54

Resposta

R R = 1,54

Exercício Resolvido #4

Elaboração própria

Calcule a Razão de Refluxo Interna pelo método Ponchon-Savarit sabendo que x d = 0,86 .

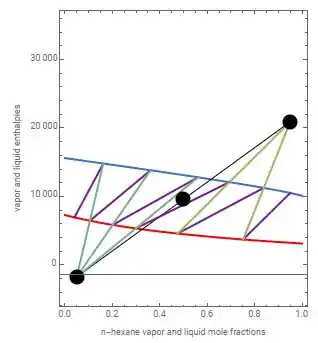
Passo 1

A questão nos deu um gráfico em que todos os estágios já foram determinados, conforme o procedimento que vimos antes.

Ela nos pede para calcular a Razão de Refluxo Interna que já sabemos que tem a seguinte fórmula:

R R i n t e r n a = L o V 1 = H ∆ D - H 1 H ∆ D - h o

Então, precisamos encontrar os elementos no gráfico para calcular nossa R R i n t e r n a .

Passo 2

Pelo gráfico, conseguimos encontrar diretamente os valores de H 1 e h o . Marcando o valor de x d = 0,86 no gráfico, conseguimos encontrar, ainda, o valor de H ∆ D . Ficando com:

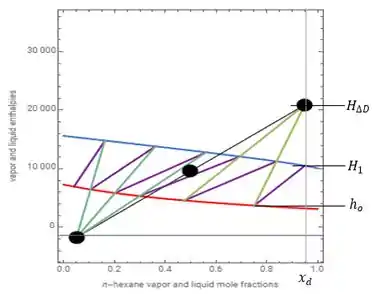
Logo,

H 1 = 10500   K J / m o l

h o = 3950   K J / m o l

H ∆ D = 20600   K J / m o l

Passo 3

Como os valores de H ∆ D ,   H 1   e   h o conseguimos encontrar a Razão de Refluxo Interna:

R R i n t e r n a = H ∆ D - H 1 H ∆ D - h o = 20600 - 10500 20600 - 3950

Então,

R R i n t e r n a = 0,61

Resposta

R R i n t e r n a = 0,61

Exercício Resolvido #5

Adaptada – Lista de Operações Unitárias I - UFF – Professor Jorge

Calcule a Razão de Refluxo mínima pelo método Ponchon-Savarit sabendo que x d = 0,9 .

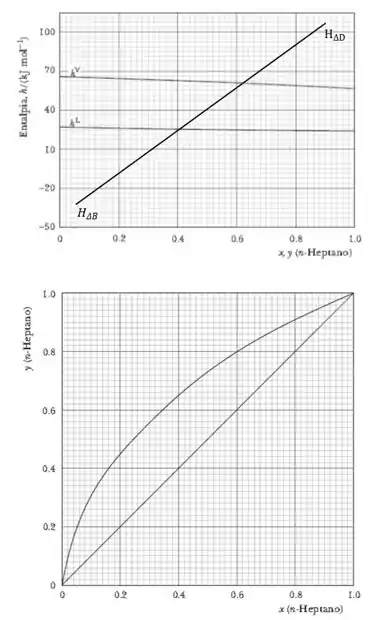
Passo 1

A questão nos forneceu o gráfico do diagrama xy e o gráfico do diagrama de fases. E nos é pedido para calcular a Razão de Refluxo mínima que já sabemos que tem a seguinte fórmula:

R R = L o D = H ∆ D m í n i m o - H 1 H 1 - h o

Então, precisamos encontrar os elementos no gráfico para calcular nossa R R .

Passo 2

Para pegar os pontos que queremos, vai ser necessário determinar a linha de amarração que passa pelo ponto de carga e estender essa linha para determinar o H ∆ D m í n i m o , como vimos na teoria. E ficamos com:

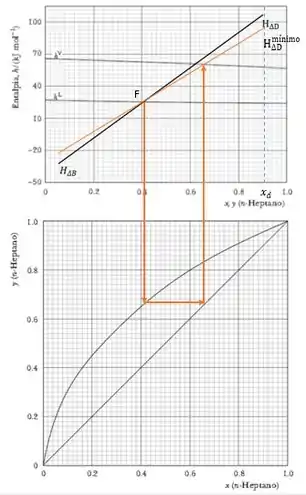
Repara que, eu marquei o valor de x d com uma linha tracejada em azul para nos facilitar ao pegar o valore desejado. Com isso, encontramos H ∆ D m í n i m o = 9 6,25   K J / m o l ;

Passo 3

Precisamos, também, marcar os valores de H 1 e h o no gráfico. Sendo estes, o encontro de x d com a curva de vapor e de líquido, respectivamente.

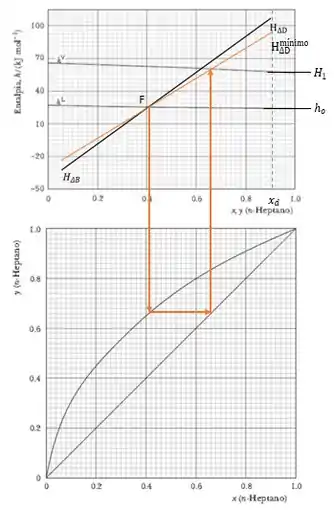
Assim, temos que H 1 = 58,75   K J / m o l   e h o = 2 5   K J / m o l

Passo 4

Como os valores de H ∆ D m í n i m o ,   H 1   e   h o conseguimos encontrar a Razão de Refluxo Interna:

R R = H ∆ D m í n i m o - H 1 H 1 - h o = 9 6,25 - 58,75 58,75 - 25

Então,

R R = 1,11

Resposta

R R = 1,11

Exercício Resolvido #6

Adaptada – Lista de Operações Unitárias I - UFF – Professor Jorge

500   k m o l / h de uma mistura binária, contendo 40 % molar da espécie volátil e em seu ponto de bolha, devem ser separados em uma coluna de pratos que opera a 1   a t m e que possui um condensador total e um refervedor parcial. A coluna deve operar em regime permanente, gerando um destilado com 90 % molar da espécie leve e um resíduo 5 % molar dessa mesma espécie.

Utilizando o método de Ponchon-Savarit e os diagramas entalpia-composição e xy apresentados na figura abaixo, responda qual o número de estágios de equilíbrio necessários, para uma vazão de refluxo 30% maior que a razão de refluxo mínima, sendo R R = 1,11 .

Passo 1

Dessa vez a questão está nos pedindo para determinar o número de estágios a partir de uma Razão de Refluxo dada. Então, precisamos encontrar o novo valor de H ∆ D para traçar nossa nova reta e desenhar os estágios.

Então, vamos novamente utilizar a equação vista na teoria:

R R = H ∆ D - H 1 H 1 - h o

Passo 2

O enunciado nos fornece o valor da Razão de Refluxo mínima do gráfico:

R R = 1,11

E nos disse que a nova razão de refluxo é 30 % maior que a Razão de Refluxo mínima.

Então,

R R 1 = 1,3   R R

R R 1 = 1,3 × 1,11

R R 1 = 1 , 44

Passo 3

Já com o valor da nossa nova Razão de Refluxo, podemos jogar na fórmula e encontrar o nosso novo H ∆ D .

R R 1 = H ∆ D 1 - H 1 H 1 - h o

Mas, para isso, ainda precisamos encontrar os valores de   H 1 e h o . Esses, nós encontramos diretamente no gráfico e tem seus valores independentes da Razão de Refluxo adotada, beleza?

Indo no gráfico, ficamos com H 1 = 58,75   K J / m o l   e h o = 25   K J / m o l .

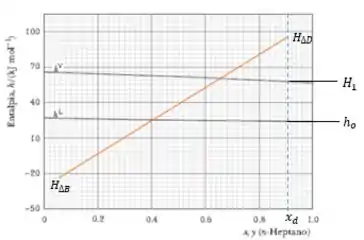
Passo 4

Agora sim podemos voltar a fórmula e encontrar nosso H ∆ D 1 .

R R 1 = 1,44 = H ∆ D 1 - H 1 H 1 - h o

1,44 = H ∆ D 1 - 58,75 58,75 - 25

H ∆ D 1 = 107,35   K J / m o l

Passo 5

Agora que já temos todos os valores necessários, vamos determinar o número de estágio da mesma forma que vimos antes e ficar com o seguinte:

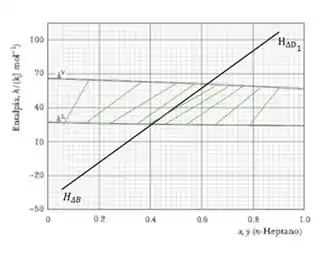
Sendo assim, são necessários 9 estágios de equilíbrio.

Resposta

9 estágios.

Exercício Resolvido #7

Adaptado - Caderno de Operações Unitárias I – UFF – Professor Jorge

Sabendo que uma coluna de destilação é alimentada com 100   k m o l / h de uma mistura com 50 % n-heptano e 50 % etilbenzeno, em seu ponto de bolha. Calcule o valor de H Δ D dado H ∆ D m í n i m o = 85   K J / m o l .

Especificação: R R R R m i n = 1,5 e H 1 = 58,75   K J / m o l

Passo 1

A questão nos pede para calcular o valor de H Δ D   dando o valor de H Δ D m i n e fornecendo a relação entre as Razões de Refluxo. Então precisamos aqui, trabalhar com as equações de refluxo que vimos na teoria.

Tanto a Razão de Refluxo operacional,

R R = L o D = H ∆ D - H 1 H 1 - h o

Como a Razão de Refluxo mínima,

R R = L o D = H ∆ D m í n i m o - H 1 H 1 - h o

Aqui a questão adotou a Razão de Refluxo mínima como   R R m i n para facilitar na hora de escrever, mas a equação é a mesma, beleza?

Passo 2

Como a questão não me deu o gráfico eu não tenho como encontrar o valor de h o então nós vamos manipular a equação de uma forma que podemos “sumir” com ele.

Além disso, eu também não sei o valor de R R ou   R R m i n , mas sei a razão entre eles. Então, vamos dividir uma equação pela outra.

R R R R m i n = H ∆ D - H 1 H 1 - h o H ∆ D m í n i m o - H 1 H 1 - h o

Simplificando isso, ficamos com:

R R R R m i n = H ∆ D - H 1 H ∆ D m í n i m o - H 1

Passo 3

Agora que não dependemos mais de h o , podemos calcular o valor de H ∆ D substituindo os valores que temos.

R R R R m i n = 1,5 = H ∆ D - 58,75 85 - 58,75

H ∆ D = 98,24   K J / m o l

Resposta

H ∆ D = 98,24   K J / m o l

Exercício Resolvido #8

Adaptado - Lista de Operações Unitárias I – UFF – Professor Jorge

Uma mistura binária contendo 50 % molar da espécie mais volátil é alimentada, em seu ponto de bolha, a uma coluna de pratos que opera à pressão atmosférica. Deseja-se que a fração molar da espécie mais volátil seja 95 % molar no destilado e de 5 % molar no resíduo. A coluna utiliza um condensador parcial com retirada de vapor e um refervedor parcial. Utilizando o método de Ponchon-Savarit e o diagrama entalpia-composição fornecidos para o sistema, determine o valor da razão de refluxo mínima.

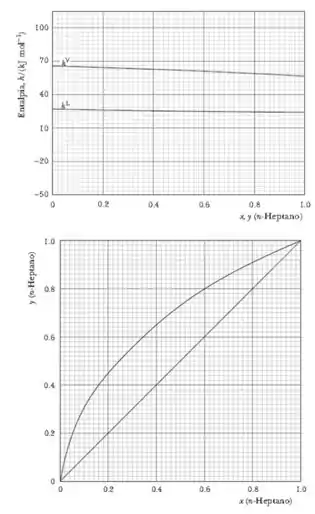
Passo 1

A questão nos forneceu o gráfico do diagrama xy e o gráfico do diagrama de fases. E nos é pedido para calcular a Razão de Refluxo mínima que já sabemos que tem a seguinte fórmula:

R R = L o D = H ∆ D m í n i m o - H 1 H 1 - h o

Então, precisamos descobrir os valores dos elementos da equação.

Passo 2

A partir do y d = 0,95 , fornecido pela questão, conseguimos encontrar o valor de x 1 pelo diagrama xy, pois o y d e o x 1 estão em equilíbrio. Assim, encontramos x 1 = 0,89 .

Para x 1 = 0,89 ,   na curva de líquido saturado, h o = 25   K J / m o l , para y d = 0,95 ,   na curva de vapor saturado, H ∆ D = 58   K J / m o l . E para z f = x = 0,5 ,   y = 0,73 , pelo diagrama xy.

Interligando os pontos x = 0,5 e y = 0,73 por uma reta, obtém-se que em x d = 0,95 ,   H = H ∆ D m í n i m o = 94,4   K J / m o l

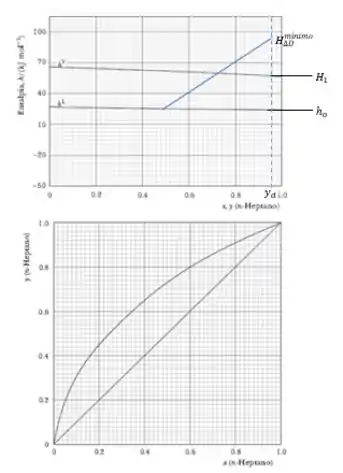
Passo 3

Agora que já encontramos todos os dados necessários, podemos jogar na fórmula.

R R = H ∆ D m í n i m o - H 1 H 1 - h o = 94,4 - 58 58 - 25

R R = 1,1

Resposta

R R = 1,1