Dados os números reais , e , calcular as raízes de uma equação do 2º grau na forma .
Observações:
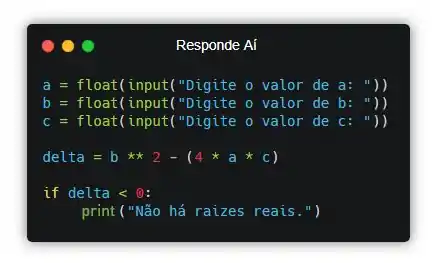
- Caso , o programa deverá imprimir a seguinte frase: “Não há raízes reais.”.
Passo 1
Beleza, para calcularmos as raízes de uma equação do 2º grau, basta nos recordarmos da famosa fórmula de Bhaskara:
Passo 2
Agora que já nos familiarizamos com a parte matemática, está na hora de declararmos as variáveis que armazenarão os dados de entrada do nosso programa:
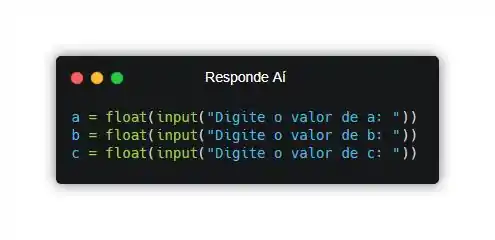
Passo 3
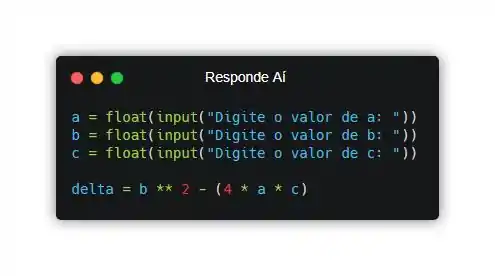
Com essas variáveis declaradas, podemos agora declarar a variável e inicializá-la com a expressão :
E já aproveitando que temo o valor de podemos agora mesmo cuidar da observação fornecida pelo enunciado, que é o caso em que :
Passo 4
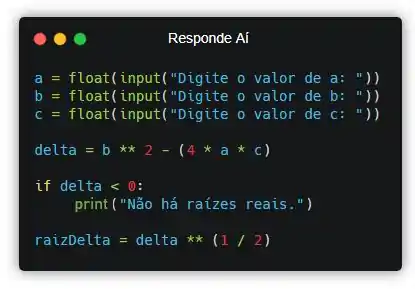
Continuando com o código, para evitarmos repetições, podemos declarar uma variável chamada que nos ajudará no cálculo das raízes da função:
Passo 5
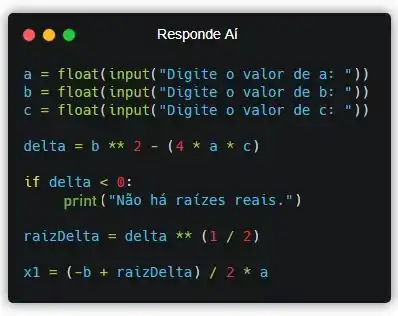
Até que enfim, podemos calcular o valor de que no código será representado pela variável :
Passo 6
Porém, antes de calcularmos vamos verificar se , isso fará com que economizemos computação. Pois, se , e nós já temos o valor de .
Para isso, basta fazermos o seguinte:
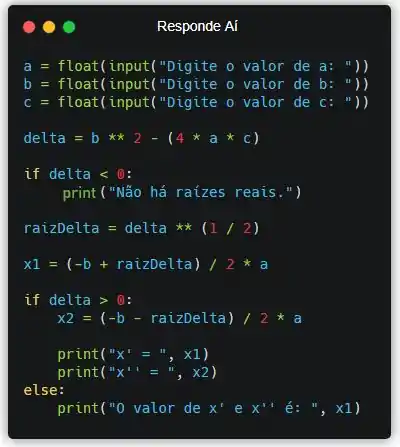
Onde, se calcularemos e realizaremos a impressão de e logo em seguida. Caso contrário, não computaremos o valor de e apenas imprimiremos o valor de afirmando que as duas raízes são iguais.
Resposta
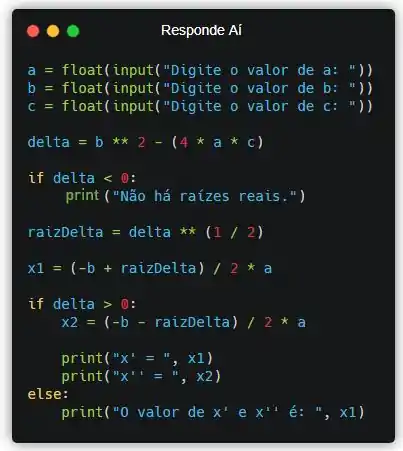
Portanto, o código para o cálculo das raízes de uma função do 2º grau é: