Ampliação de Escala
Produzido por Marcelo AlvesTeoria
Introdução
É muito comum que a gente não tenha que projetar um agitador do zero e sim mudar a escala dele. Um exemplo é, a partir de um agitador em escala de laboratório, passar à uma escala industrial.
Vamos fazer essa mudança de escala amarrando algumas condições nas duas escalas, isto é, igualando algumas coisas nas duas escalas. O que amarramos está ligado ao objetivo da agitação.
Há, basicamente, 3 semelhanças que podemos usar:
- Semelhança geométrica
- Semelhança fluidodinâmica
- Manutenção do nível de agitação
Bora ver agora cada uma delas.
- Semelhança geométrica
- Semelhança fluidodinâmica
- Manutenção do nível de agitação
Esse é o critério mais básico e geralmente sempre é atendido. Chamando uma escala de “” e a outra de “”, temos as seguintes relações:
Um detalhe importante é que mantemos o tipo do impelidor.
Quando vamos pra semelhança fluidodinâmica, partimos do princípio que respeitamos a semelhança geométrica, que é a mais básica de todas.
A semelhança fluidodinâmica visa manter o comportamento da mistura; como há, basicamente, dois regimes de escoamento (laminar e turbulento) e o equacionamento pra eles é diferente, vamos ter que analisa-los em separado.
Regime Laminar
Nesse regime, vale:
Podemos isolar o
E como o impelidor é o mesmo e é um parâmetro que depende do impelidor:
Daí:
Usando as definições de e :
Regime Turbulento
No regime turbulento, vale:
Como a semelhança geométrica foi respeitada:
Daí, usando a definição de :
Se queremos manter o nível de agitação, precisamos da igualdade dos números de agitação nas duas escalas:
Ou, usando a definição de :
Novamente, temos que abrir agora nos dois casos de regimes de escoamento.
Regime Laminar
Se respeitada a semelhança geométrica, vamos substituindo definições e chegamos em:
Regime Turbulento
Já para o regime turbulento, podemos expressar a semelhança no nível de agitação como:
Regime Laminar
Regime Turbulento
Regime Laminar
Regime Turbulento
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Quais os três tipos de semelhanças mais utilizadas para realizar mudança de escala? Diga também o que cada tipo leva em conta.
Passo 1
Como vimos lá na teoria, os 3 tipos de semelhança mais usados são:
- Semelhança geométrica
- Semelhança fluidodinâmica
- Manutenção do nível de agitação
Explicando cada um deles:
- Na semelhança geométrica mantemos constantes razões entre medidas na geometria do tanque nas duas escalas, mantendo constante o TIPO de impelidor. Avaliamos geralmente as seguintes relações:
- Ao avaliar semelhança fluidodinâmica, queremos manter o comportamento da mistura. Ao analisar fluidodinâmica, partimos do princípio que a semelhança geométrica foi respeitada e vamos querer, além das razões entre comprimentos, que as razões entre forças nas duas escalas sejam respeitadas.
- E falar em manutenção de nível de agitação é bem rápido. Queremos que:
E ah! Lembra que o equacionamento pra semelhança fluidodinâmica varia dependendo se o regime de escoamento é laminar ou turbulento.
Lembrando que é o nível de agitação.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Um certo processo fermentativo é realizado por células em um reator em escala piloto. Para manter o meio homogêneo, é necessária agitação. Entretanto, deve-se tomar cuidado! Células são sensíveis e se a agitação for muito intensa, pode-se matá-las. Há um limite da força que as células conseguem suportar.Deseja-se ampliar a escala do processo para um reator industrial. Sabendo-se das necessidades do processo, o que deve ser avaliado para a mudança de escala?
Passo 1
Já vimos que há três tipos de semelhança que são geralmente usadas na hora de fazer mudança de escala:
- Semelhança geométrica
- Semelhança fluidodinâmica
- Manutenção do nível de agitação
O enunciado diz que células são sensíveis e há um limite da força que as células conseguem suportar. Daí o critério que deve ser avaliado é principalmente a semelhança fluidodinâmica, pois este critério avalia as forças no sistema.
E, como vimos na teoria, a semelhança geométrica é a mais básica das semelhanças, então esta também deve ser respeitada.
Já a manutenção do nível de agitação fica em segundo plano... Não podemos a priorizar porque, talvez, manter o nível de agitação geraria uma força superior ao que as células podem suportar.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Cremaso, Marco Aurélio. Operações unitárias em sistemas particulados e fluidomecânicos, 2 ° e d - Adaptado
Calcule o valor da potência útil ao se reduzir pela metade o valor do número de rotações de rotações do impelidor referente a um tanque com chicanas. As únicas informações disponíveis do sistema original são:
Passo 1
Essa questão é um exemplo de que não necessariamente precisa mudar o tanque para mudar a escala. Aqui a escala foi mudada devido à mudança do número de rotações do impelidor.
E repara que, ao mudar o número de rotações, estamos mudando também o número de Reynolds do impelidor, já que:
E, ao mudar o Reynolds do impelidor, há mudança fluidodinâmica no sistema.
Algo que temos que notar é que há semelhança geométrica nas duas situações, até porque nem chegamos a mudar o tanque.
Para a mudança de escala, vamos usar a semelhança fluidodinâmica.
Passo 2
Na situação original, o número de Reynolds era
Com:
Como o número de rotações, , que é diretamente proporcional a , foi reduzido pela metade, o novo Reynolds será:
Dando uma olhada na curva b do gráfico para curva de potência, já que o impelidor é de pás retas e há chicanas no tanque.
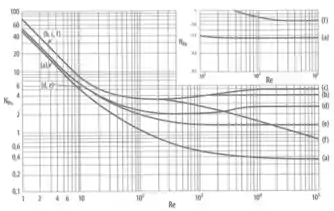
Vemos que esse valor de número de Reynolds corresponde a regime turbulento. Daí, a semelhança fluidodinâmica pode ser expressa por:
Como o fluido do processo é o mesmo nos dois casos, a densidade, , é a mesma. Ficamos com:
E, como o diâmetro do impelidor é o mesmo nos dois casos, podemos cortar os também”
Passo 3
Como estamos interessados na potência útil no caso 2, bora isolar esse termo:
O enunciado diz que o número de rotações foi reduzido pela metade, daí:
Substituindo isso, ficamos com:
E agora é só fazer conta haha Como na situação inicial :
Resposta
Exercício Resolvido #4
Cremaso, Marco Aurélio. Operações unitárias em sistemas particulados e fluidomecânicos, 2 ° e d - Adaptado
Obtenha o valor da potência útil, bem como projete o sistema de agitação, para tratar litros de efluente, mantendo o mesmo nível de agitação. A referência é o seguinte sistema de agitação, em que o volume do tanque é projetado para ser maior do que o volume de líquido:

Repare, pelas relações geométricas utilizadas, que o sistema de referência é padrão.
Sabe-se, também, que é borbulhamento de ar nos dois sistemas, que a agitação é intensa e que:
Passo 1
Já tínhamos feito um projeto e agora temos que ampliar a escala.
Podemos escrever o volume de líquido como:
Como há borbulhamento de gás, usamos:
Daí:
Vou trabalhar no sistema de unidades CGS, daí, litros vale .
Calculando o diâmetro do tanque:
A partir do valor de , poderíamos calcular as demais medidas com base nas proporções padrão, assim como foram obtidas pra o projeto de referência. Entretanto, podemos nos basear, alternativamente, na semelhança geométrica, que é como vou seguir.
Passo 2
Usando a semelhança geométrica para obter as outras medidas do tanque:

Passo 3
Como a agitação é intensa, vamos considerar que o regime é turbulento. Daí, usamos para a semelhança geométrica:
Partindo do princípio que o fluido é o mesmo nos dois casos, a densidade é a mesma.
E podemos, daqui, tirar o novo número de rotações, , do impelidor. Isolando-o:
O lance é que ainda não sabemos :/ Masssss, como o enunciado diz que há manutenção do nível de agitação:
Substituindo os valores que temos:
Agora que temos o valor de , podemos voltar e calcular o :