Hidrociclones
Produzido por Marcelo AlvesTeoria
Opaa! Seja bem vindo ao Responde Aí! Bora bater um papo sobre hidrociclones?!
O que é um Hidrociclone?
O hidrociclone é um equipamento de separação sólido-líquido onde a separação ocorre através da força centrifuga. Ele tem essa carinha aqui:
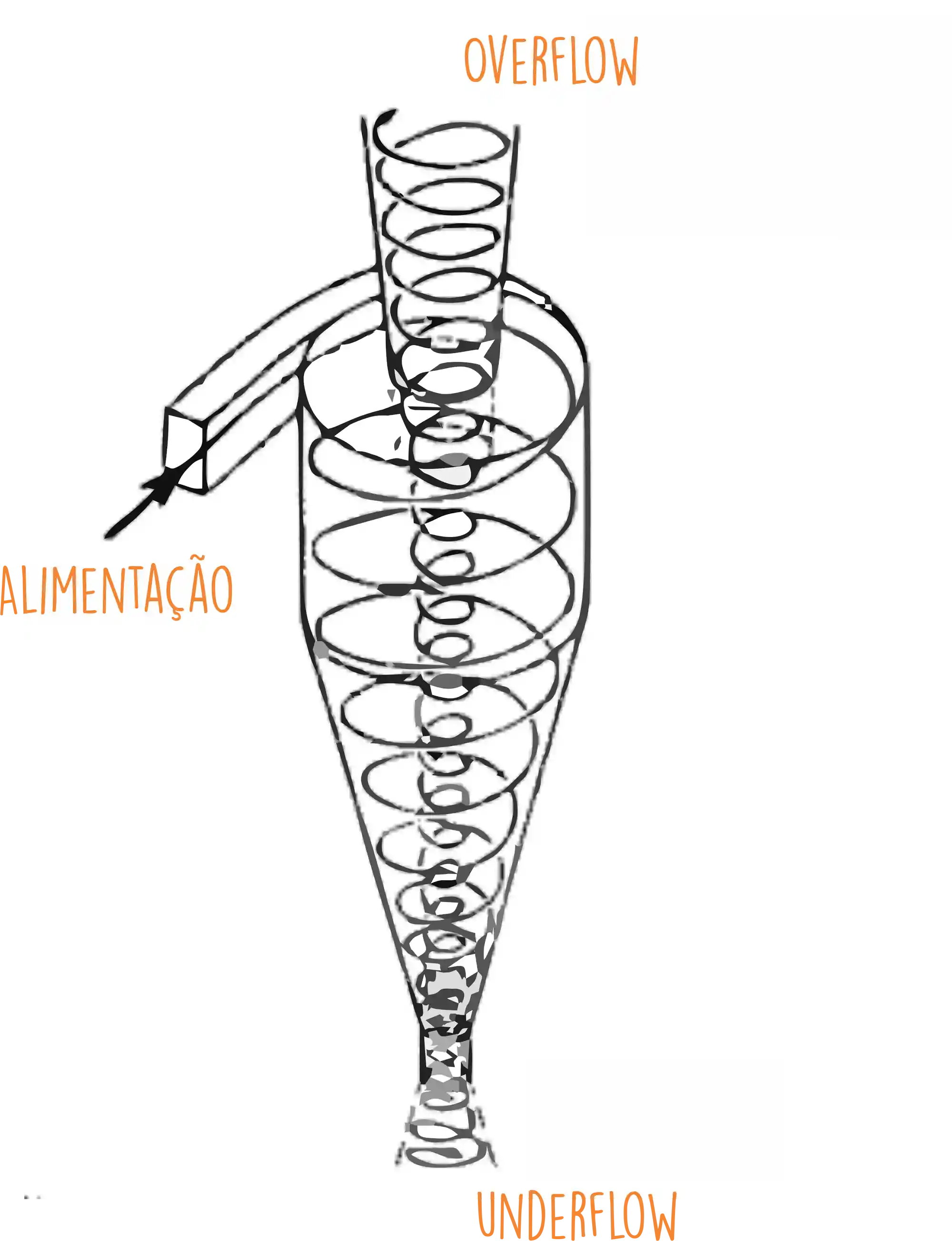
Na alimentação temos a mistura de sólido e líquido e após a separação a carga pesada sai por baixo, chamamos ela de underflow e a carga leve é o overflow que sai por cima!
Os hidrociclones são bem parecidos com os ciclones, suas geometrias são semelhantes e a ideia de funcionamento também. Mas temos que nos atentar com as duas diferenças principais:
- Nos ciclones a separação é gás-sólido, ou seja o fluido é um gás;
- A razão de fluido nos ciclones é igual a zero, já nos hidrociclones, o
é diferenete de zero. Mas isso é conversa pra daqui a pouco!
Nesse vídeo abaixo a gente te explica tudo o que você precisa saber sobre hidrocilones, como é o seu funcionamento, como dimensionar e mais! Dá só uma conferida 👇
Como Funciona um Hidrociclone
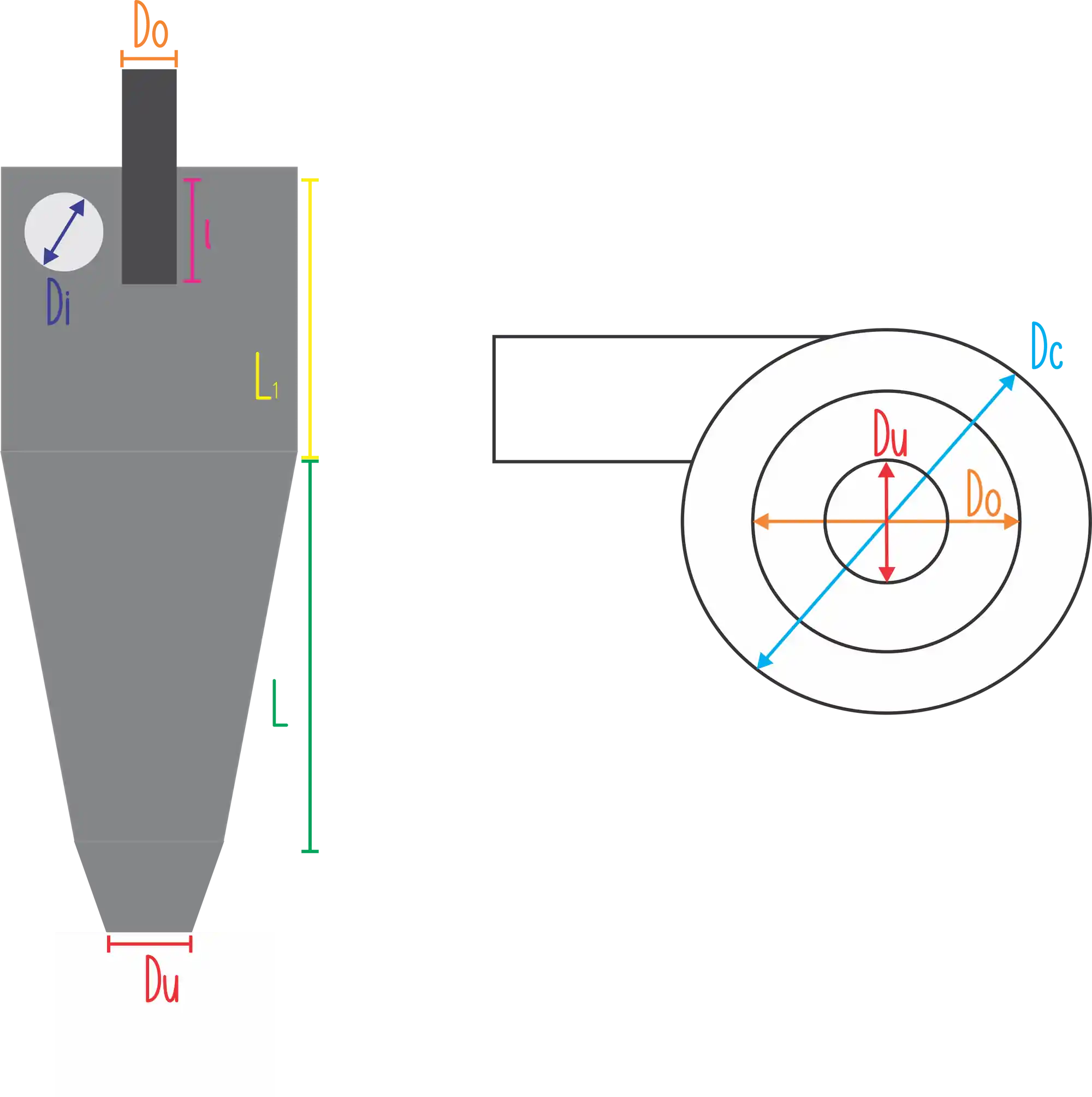
Nessa figura abaixo você pode observar um desenho esquemático com a geometria de um hidrociclone:
O
A separação no hidrociclone acontece devido à alimentação tangencial na sua parte cilíndrica. É formado um movimento em espiral descendente que arrastasta as partículas maiores e mais pesadas para saída inferior do equipamento (underflow). Já as partículas menores e menos densas são arrastadas para o centro do equipamento, onde forma-se um movimento em espiral ascendente e estas saem por um orifício superior (overflow).
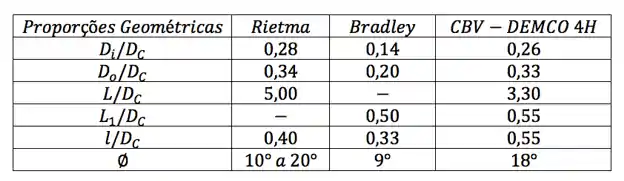
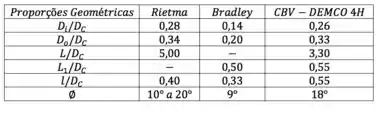
Na tabela abaixo você pode observar as relações geométricas do hidrociclone:
Queda de Pressão em um Hidrociclone
A queda de pressão em um hidrociclone pode ser calculada pela equação de Euler, que é dada por:
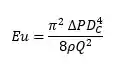
Além da correlação:
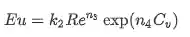
Usamos os seguintes os parâmetros da equação de Euler:

Você também pode conferir esse conteúdo em vídeo!
Razão de fluido
A razão de fluido é o quanto da vazão de fluido que sai no concentrado dividido pela vazão de fluido que entra. Ou seja:
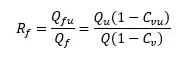
Esse
Para esse cálculo precisamos da correlação de razão de fluido:
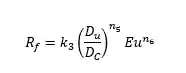
Abaixo temos tabelados os parâmetros da equação:

Cálculo do diâmetro de corte reduzido
O diâmetro de corte reduzido é o diâmetro associado com a eficiência granulométrica reduzida igual a 50%. Aqui trabalhamos com os “reduzidos” porque há
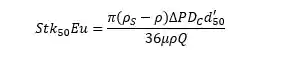
Usamos também a seguinte correlação:
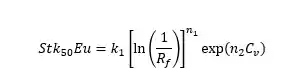
Parâmetros da equação:

Dimensionamento de um Hidrociclone: Correlações Importantes
Para o dimensionamento de um hidrociclone qualquer, usamos as seguintes correlações:
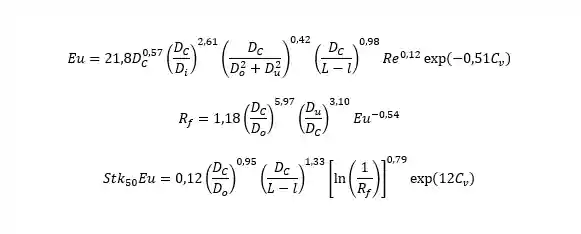
Eficiência Granulométrica Reduzida
Pela eficiência granulométrica reduzida (G') conseguimos avaliar a performance de um hidrociclone. Ela pode ser calculada a partir da seguinte fórmula:
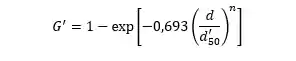
Com n=3 para hidrociclones.
Agora vamos praticar com exercícios?!
Como Funciona um Hidrociclone
Queda de Pressão em um Hidrociclone
Razão de fluido
Cálculo do diâmetro de corte reduzido
Dimensionamento de um Hidrociclone: Correlações Importantes
Eficiência Granulométrica Reduzida
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Qual a principal diferença operacional entre ciclones e hidrociclones? Discuta, também, sobre a erosão em cada um desses equipamentos.
Passo 1
Tanto ciclones como hidrociclones são equipamentos que fazem uso de um campo centrífugo gerado pelo próprio movimento do fluido para obter a separação de partículas do fluido.
Mas há uma grande diferença operacional em termos do fluido alimentado em cada um dos equipamentos, e é isso que o enunciado pergunta. Em ciclones, o fluido da suspensão alimentada é um GÁS, enquanto nos hidrociclones, o fluido da suspensão é um LÍQUIDO.
Passo 2
O enunciado também pede pra gente comentar sobre a erosão em cada um dos equipamentos. Pensa comigo, o principio de separação nos dois equipamentos é semelhante, certo? Tem uma suspensão se movimentando em espiral num equipamento com uma parte cilíndrica e uma parte que é um tronco de cone e as partículas são separadas devido a um campo centrífugo.
Se os equipamentos e forma de separação são tão parecidos, poderíamos pensar, a princípio, que a erosão também seria semelhante, né? Massssssss acontece que não é. E isso ocorre justamente pelo tipo de fluido em cada um dos equipamentos.
A erosão no equipamento ocorre devido ao atrito das partículas sólidas com o equipamento. Mas, como vimos, esses sólidos estão em suspensão, daí imersos em um fluido. Diferentes fluidos podem “atenuar” a erosão... quanto maior a viscosidade do fluido, é como se ele impedisse que a partícula sólida se esfregasse com tanta força no equipamento, e assim diminui a erosão.
Líquidos possuem viscosidade muito maior do que gases e como hidrociclones operam com líquido e ciclones com gases, a erosão é mais intensa em ciclones do que hidrociclones.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
UFRJ – Lista 4, Prof. Medronho
Uma indústria química utiliza um hidrociclone para tratar de uma suspensão aquosa, a em volume de . Determine a eficiência de separação.
Dados:
, , ,
Configuração do hidrociclone:
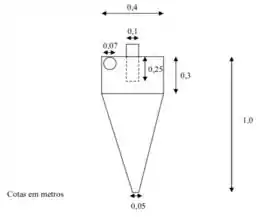
Passo 1
Temos que determinar a eficiência de separação obtida usando esse hidrociclone aí. Antes de qualquer coisa, temos que saber qual é a família desse hidrociclone pra saber quais equações e parâmetros usar. Lá na teoria, eu coloquei uma tabelinha com as proporções geométricas em cada uma das famílias. Vamos calcular para esse hidrociclone aí e ver se ele se encaixa em alguma família.
Calculando
Opa! Já sabemos que esse hidrocilone não tem família; ele é um hidrociclone qualquer então temos que usar as equações pra um hidrociclone qualquer.
E, para chegar na eficiência total de coleta: temos como, pelas equações, calcular ; como sabemos a expressão de em função de (vou usar a equação de Rosin-Rammler-Bennett modificada), teremos a expressão de “completa”. Depois, calculamos e depois .
Ah! Vou adotar o CGS então já vou listar os dados convertendo-os para o CGS, caso necessário:
Passo 2
Primeiro de tudo, vamos ter que calcular o diâmetro de corte reduzido, Em hidrociclones, trabalhamos majoritariamente com , e , e ficamos variando entre as definições e as correlações. Vou escrever aqui embaixo as duas formas (genéricas) de cada um deles (definição e correlação):
Repara que a expressão que envolve é a definição de ; daí podemos calcular pela correlação (termo da direita) e depois relacionar com a definição. Mas, antes disso, preciso de ; como não tenho , tenho que calcular pela correlação e, para isso, preciso de . Daí a primeira coisa que vou calcular é , certo? Tenho tudo da definição então é ela que vou usar:
Repara que eu lancei o em centímetros.
Calculando :
Calculando pela correlação:
Relacionando com a definição:
Substituindo os valores:
Passo 3
Vamos usar, para a expressão da eficiência granulométrica, a equação de Rosin-Rammler-Bennett modificada:
Com para hidrociclones
Já sabemos o valor de e de . A questão é que para encontrarmos o valor da eficiência global reduzida , vamos ter que integrar em :
Daí, precisamos de uma expressão para em função de . Vamos obtê-la da curva que o enunciado deu:
Aplicando dos dois lados:
Substituindo isso na equação de :
Agora, integramos na calculadora:
Mas o enunciado pede eficiência global e não a eficiência global reduzida ; sabemos que:
Daí:
Só uma análise do resultado: faz sentido ? Sim ! A vazão associada com a razão de fluido é como se tivesse de coleta, já que ela carrega partículas com a mesma distribuição original e isso faz com que a eficiência global do separador aumente.
Resposta
Exercício Resolvido #3
Dimensionar o hidrociclone Rietma capaz de tratar de uma suspensão de a em volume. A queda de pressão de operação será de e o diâmetro de corte reduzido que se deseja obter é .
Dados: e
Passo 1
Em ciclones, para dimensionar bastava calcular o porque todas as outras dimensões eram função dele. Já aqui em hidrociclones, com conseguimos amarrar todas as outras dimensões, com EXCEÇÃO DE (que vai estar relacionado à coleta de partículas e a concentração da corrente concentrada) .Então temos que calcular .
Reunindo as informações que temos:
e
Passo 2
Em hidrociclones, trabalhamos majoritariamente com , e , e ficamos variando entre as definições e as correlações. Vou escrever aqui embaixo as duas formas (genéricas) de cada um deles (definição e correlação):
Nós não sabemos nem e nem , mas repara que sabemos tudo da linha do Euler, com exceção de , que queremos calcular:
Usando aquelas tabelas da teoria pra obter os valores dos parâmetros:
E Reynolds é:
Substituindo:
Rearranjando:
Elevando os dois lados a , dá aproximadamente:
Escolhendo trabalhar com o CGS temos:
Repara que eu converti na equação mesmo.
Passo 3
Agora falta o . Repara que a partir de dá pra calcular o , mas não sabemos ainda quem é o .Masssss repara que temos como calcular o pela correlação para :
“Mas eu não sei quem é ” Verdade, mas tem como calcular pela definição:
Juntando tudo, já substituindo os parâmetros:
Daí:
Passo 4
Voltamos para . Temos outro “probleminha”; agora sabemos , mas ainda não sabemos . Então, bora usar a definição dele pra calcular:
Agora sim, voltando pra correlação de e já substituindo os parâmetros para o Rietma:
Substituindo o que temos:
Resposta
Exercício Resolvido #4
UFRJ – Lista 4, Prof. Medronho
Devido a alterações ocorridas em um processo utilizado por uma indústria, um hidrociclone Rietma de de diâmetro terá suas variáveis operacionais modificadas para , , . Sabendo que a distribuição granulométrica do material particulado na alimentação é . Pede-se calcular a vazão de operação e a eficiência total, sabendo-se que e que o fluido de operação é a água com as seguintes propriedades: e .
Passo 1
Esse enunciado foi bem bonzinho com a gente: já deu em função de (pra quando a gente for integrar em ) e já deu as propriedades físicas do fluido de cara haha Mas bora ver o que ele quer.
Temos um hidrociclone Rietma com algumas especificações: , , ; sabemos, também, que a concentração na entrada é .
Sabemos, também, que , e .
Vamos ter que calcular a vazão de operação e a eficiência total de separação ; pra isso é só aplicar fórmula porque tá tudo amarradinho.
Passo 2
Em hidrociclones, trabalhamos majoritariamente com , e , e ficamos variando entre as definições e as correlações. Vou escrever aqui embaixo as duas formas (genéricas) de cada um deles (definição e correlação), para quando o hidrociclone é de alguma família:
A primeira coisa que vou calcular é a vazão logo. Eu não tenho e nem , então não vou pensar em usar as expressões de pra isso. Também não tenho ou pra pensar em usar a linha do . Sobra usar as expressões para .
Como não tenho o valor de , vou escrevê-lo em função de :
Ah! Vou precisar passar para o CGS antes de jogar na fórmula, já que escolhi trabalhar no CGS.
Voltando para as expressões pra , já com os parâmetros da correlação para o Rietma:
Passo 3
O enunciado também pediu pra gente calcular a eficiência total , mas pra chegar lá ainda temos um caminho pra percorrer haha Olha só: o que temos pra começar a calcular a eficiência é a equação de RRB modificada:
Tendo a expressão completinha de e com em função de , podemos integrar e calcular :
Como o que queremos é , vamos usar:
Massss, não temos a expressão de RRB “completinha”; falta achar o . Pra isso, vamos pelo :
Como não temos o valor de e nem o de , temos que calcular o valor de pela correlação (termo da direita); pra isso, preciso de :
Não tenho , então tenho que usar a correlação (termo da direita); para isso, preciso calcular . Vou pela definição mesmo, já que sei tudo:
Calculando pela correlação, já com os parâmetros adequados:
Voltando pra , já com os parâmetros adequados:
Igualando esse valor com a definição de , encontramos :
Passo 4
Agora que temos , podemos escrever a expressão de completinha. Já com o em função de (foi dado):
Fazendo, na calculadora a integral:
Como queremos :
Resposta
Exercício Resolvido #5
UFRJ – Lista 4, Prof. Medronho
Uma bateria de hidrociclones Bradley, de de diâmetro, é utilizada para tratar de uma suspensão aquosa, a em volume de . Calcular:
- O número de hidrociclones necessários
- A eficiência total de separação
- A concentração volumétrica no underflow
Dados:
; ; ;
Distribuição granulométrica do material particulado na alimentação:
![]()
Passo 1
Temos hidrociclones com , e especificados; ele está todo amarrado e a vazão que passa por um desses hidrociclones está amarrada também! Como precisa tratar uma vazão , vamos ter que calcular o número de hidrociclones necessários.
Para o cálculo da eficiência total de separação, vamos ter que primeiro calcular , aí jogá-lo na expressão de ; como vou usar equação de Rosin-Rammler-Bennett modificada (RRB):
Depois, achamos por meio de:
Lembrando que colocar em função de na expressão de ; para tal, vamos precisar de uma expressão para em função de , que podemos achar pela tabela que ele deu com pares . Vamos ter que usar os em base unitária.
![]()
E, como o enunciado pede eficiência total e não eficiência total reduzida, calculamos usando:
Já para o cálculo da concentração do underflow, vamos ter que calcular a quantidade de partículas que sai no underflow e a quantidade de fluido que sai no underflow; depois é só aplicar a definição de .
Ah! Repara que o enunciado não deu para o fluido, mas disse que é água a então podemos ir atrás de informação tabelada:
Já passei a viscosidade pra Poise porque vou escolher trabalhar no CGS.
Passo 2
a) Em hidrociclones, trabalhamos majoritariamente com , e , e ficamos variando entre as definições e as correlações. Vou escrever aqui embaixo as duas formas (genéricas) de cada um deles (definição e correlação), para quando o hidrociclone é de alguma família:
A primeira coisa que vamos calcular é a vazão passando pelo nosso hidrocilone. Não vou usar porque não tenho nem pra usar a definição e nem pra usar a correlação. Não vou usar porque não tenho pra usar a definição e nem pra usar a correlação. Daí sobra usar . Reescrevendo essa segunda linha, já com cos parâmetros corretos:
Precisamos calcular Reynolds:
é o que a gente quer calcular então deixei em função dele. Daí, substituindo tudo que temos:
Repara que converti o de para , já que estamos trabalhando com o CGS. Calculando:
Mas temos que tratar . Não posso comparar gatos com peixes; preciso ter os dois nas mesmas unidades pra comparar.
Precisamos de hidrociclones tratando uma vazão para ter o tratamento da vazão total :
Passo 3
b) A eficiência total de separação
Vamos usar , mas precisamos de primeiro. Vamos ter que usar , que é onde ele aparece.
A definição tem o ; preciso calcular o pela correlação e depois igualar esse valor a definição pra tirar o , mas antes preciso calcular o . Usando a correlação, como os parâmetros do Bradley:
Opa! E quanto vale Euler? Vamos ter que calcular!
Podemos ir pela definição mesmo porque já sabemos tudo dela:
Voltando a :
Voltando para correlação de e já substituindo os parâmetros e valores conhecidos:
Relacionando com a definição:
Passo 4
Já podemos escrever
Mas para resolver , precisamos colocar em função de ; antes, precisamos da curva . Como o enunciado não pediu um modelo específico, vou usar o GGS para ajustar os dados:
![]()
Lembrando, o modelo GGS tem a cara:
A forma linear fica:
Fazendo regressão linear dos pares , para achar os parâmetros , obtive:
Daí:
Então:
Para isolar , primeiro elevamos os dois lados a , que dá no mesmo que .
Substituindo na expressão de :
Agora sim podemos integrar:
Como é pedida a eficiência total e não a eficiência total reduzida :
Passo 5
c) A concentração volumétrica no underflow
Pensa comigo: concentração volumétrica é volume de partículas dividido por volume de suspensão, certo? Sendo que volume de suspensão é a soma do volume de partículas e volume de fluido.
Vou adotar como base de cálculo . A gente calculou que a vazão em um hidrociclone é então, em , estamos falando de um volume de suspensão . Na entrada, , então desse volume são partículas e o resto é fluido.
Agora, vamos por partes:
Sabemos que daí desse volume de partículas foi recuperado, ou seja:
significa que do fluido alimentado sai no concentrado. Daí, junto com , sai:
Calculando :