Centrífugas
Teoria
Introdução
NÃO projetamos centrífugas! Nós selecionamos!
Oi Oi! Vamos agora falar de centrífugas. Já comecei o tópico com um spoiler sim haha Mas bora entender isso. Os equipamentos que vimos até agora são mais simples e mais baratos que centrífugas; mandar fazer uma centrífuga do jeitinho que você quer seria absurdamente caro e por isso compramos modelos já existentes; ninguém é tão rico quanto esse gatinho:
Centrífugas são equipamentos usados, majoritariamente, para separação sólido-líquido. Dentro delas, a suspensão vai girar em altas velocidades e esse giro vai gerar um campo centrífugo. Por causa desse campo centrífugo (que vai apontar na direção das paredes da centrífuga), as partículas vão se aproximando das paredes, já que tem densidade maior do que o fluido.
Tipos de centrífugas
Existem duas classes de centrífugas:
- Decantadoras: as partículas são separadas porque batem e ficam na parede da centrífuga
- Filtrantes: a centrífuga filtrante contém um filtro e, nela, fluido e partículas são lançadas em direção ao filtro pelo campo centrífugo
Ainda existem subclasses dentro de cada uma dessas. Por exemplo, em centrífugas decantadoras, a mais famosa é a tubular.
E ah! Importante: diferentemente de ciclones e hidrociclones em que se aumentasse a vazão de alimentação ia aumentar o campo centrífugo, aqui em centrífugas o campo centrífugo é constante independentemente da vazão que você use, porque ele é gerado por um motor e NÃO pela vazão alimentada.
Embora existam centrífugas que operam em batelada, operações unitárias foca mais nas contínuas, então essas que vou mostrar pra você aqui, ok? Mas antes, bora ver um conceito importante.
Intensidade do campo centrífugo: o fator g
Na hora de falar da intensidade do campo centrífugo, vamos fazer uma referência ao campo gravitacional da Terra, que tem intensidade , de forma que vamos falar que o campo centrífugo da centrífuga tem “tantos ”. Daí precisamos de uma definição:
Em que:
E só lembrando: esse termo é o campo centrífugo.
Algo bem importante é que tem que usar em . Daí vou colocar aqui em baixo a conversão de em para :
Se, por exemplo, você souber que fator g é , isso quer dizer que o seu campo centrífugo tem intensidade de , ou seja, ele tem intensidade de vezes o campo gravitacional da Terra.
Centrífugas tubulares
A primeira centrífuga que vamos ver é a tubular, que é uma casca cilíndrica girando, ou seja, tubos concêntricos de diâmetros diferentes girando. Dá uma olhada na figura abaixo, em que a suspensão ocupa a parte mais escura do desenho (entre os tubos concêntricos).
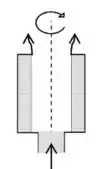
Bora ver agora como calcular a eficiência dela; pra isso, eu queria primeiro te lembrar de algo que a gente viu lá em câmaras de poeira: uma partícula que entrava em da altura e era separada no finalzinho tinha ; uma que entrasse em da altura e era separada no finalzinho tinha e assim por diante.
Isso acontecia porque consideramos partículas bem distribuídas na alimentação e, por exemplo, da altura tinha do volume aí tinha de partículas e eram essas que eram coletadas.
Aqui na centrífuga tubular é a mesma ideia. Por exemplo, a é a partícula que tem daí, é a partícula que é separada totalmente de metade do volume e fica completamente na outra metade. A questão é que aqui pra pegar metade do volume não basta olhar pro raio, tem que olhar pra área da base. Sabendo disso, uma partícula que entre num raio , com:
Vai ter G:
E só pra definir logo, o volume útil da centrífuga tubular é o volume entre os tubos concêntricos, volume que a suspensão ocupa. Sendo:
O volume útil é:
Quando usamos centrífugas, geralmente é porque queremos pegar as partículas bem pequenininhas; daí alguém supôs que o Reynolds dessas partículas seriam bem pequeninhos e elas sedimentariam na região de Stokes. Dá pra chegar em uma expressão para em função de :
Repara que, como a expressão de poderia, matematicamente, assumir valores maiores que , temos que definir por intervalos.
Duas outras expressões importantes derivadas dessa fórmula são expressões pra e :
E podemos, ainda, escrever em função de :
Se você tiver , é provável que seja mais fácil ir por essa última expressão de aqui.
Mudança de escala de centrífugas (Scale-up/ Scale-down)
“Marcelo!!! Você disse que tem vários tipos de centrífugas aí fala de uma só e já vai pra mudança de escala!?” Calmaaaaa. Você já vai entender porque eu estou “pulando” as outras.
Avaliando ainda a centrífuga tubular e rearranjando a equação do de forma a isolar e multiplicando e dividindo por , chegamos em:
Epa! Esse termo é a velocidade terminal da partícula quando o campo é o gravitacional , ou seja, esse termo é o Já o outro termo, vamos chamar de , que é um parâmetro da centrifuga (definido pela geometria dela) e tem unidade de área (comprimento ao quadrado). Daí podemos escrever:
Podemos escrever a vazão dessa forma para qualquer centrífuga; o que muda é a expressão para o . Daí podemos escrever para qualquer centrífuga : )
Para centrífuga tubular, abrindo o :
“E cadê a mudança de escala?” Quando mudamos de escala, amarramos o , daí amarramos o . Imagina duas centrífugas: 1 e 2.
Para que as duas centrífugas operem com mesmo , preciso que:
Se isolarmos eles nas expressões e igualarmos, chegamos em:
E esse é o critério pra mudança de escala. Lembra dele, hein!
Influência da vazão no diâmetro de corte
Já dei spoiler, na introdução, que aumentar a vazão na centrífuga NÃO aumenta o campo centrífugo. Agora pensa comigo: se estou aumentando a vazão, a partícula fica menos tempo na centrífuga, ou seja, o tempo de residência diminui.
E te falei que o campo centrífugo fica inalterado se eu mudo a vazão; daí a velocidade terminal das partículas fica inalterada e, por consequência, o tempo de queda fica inalterado.
Se as partículas continuam precisando do mesmo tempo pra serem separadas, ao diminuir o tempo de residência estamos prejudicando a separação, isto é, estamos diminuindo a eficiência!
Agora que já entendemos a física da questão, bora ver isso com equações; bora pensar em duas centrífugas iguais, daí com . Portanto:
Disso, dá pra chegar em:
Que é o mesmo que:
Se aplicar raiz quadrada dos dois lados, vemos melhor que o diâmetro de corte é proporcional à raiz da vazão:
Ou seja:
Explicando mais isso: se o aumenta, significa que o diâmetro associado com é maior, daí, tem uma faixa maior de diâmetros associados com pequenos, por exemplo, daí a eficiência diminuir.
Fazendo um paralelo com ciclones e hidrociclones, lá o efeito em pelo aumento da vazão era inverso:
Ou seja, aumentando a vazão, diminuía o ; isso porque o campo centrífugo aumentava mais com o aumento da vazão do que o tempo de residência diminuía.
Intensidade do campo centrífugo: o fator g
Centrífugas tubulares
Influência da vazão no diâmetro de corte ( d 50 )
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Em um laboratório, um aluno observou que seu colega, trabalhando com um hidrociclone, aumentou a vazão de suspensão a ser tratada e obteve aumento da eficiência de separação. O aluno, trabalhando com uma centrífuga tubular, resolveu, então, aumentar, também, a vazão de alimentação que ele estava tratando na centrífuga.
O que podemos prever sobre a eficiência de separação resultante?
Passo 1
Ok, bora resumir o enunciado? O garoto tá trabalhando com uma centrífuga e aumentou a vazão de suspensão alimentada. O que vai acontecer com a eficiência global?
Tanto em hidrociclones como centrífugas, a separação ocorre devido a um campo centrífugo. O lance é que nos hidrocilones (assim como em ciclones), o campo centrífugo é gerado pelo próprio movimento do fluido e nas centrífugas ele é gerado por um motor.
Lá na teoria de ciclones, a gente viu que quando aumentamos a vazão em ciclones, a eficiência de separação aumenta porque, embora o tempo de residência seja reduzido, o tempo de queda aumenta bem mais. O desenvolvimento pra hidrocilones é igualzinho, já que o princípio de separação em cilclones e hidrociclones é idêntico.
Já em centrífugas, o campo centrifugo depende apenas do motor da centrífuga e por isso fica constante independentemente da vazão alimentada. Dessa forma, quando aumenta vazão em centrífugas só vai haver o efeito do tempo de residência ser diminuído e por isso a eficiência DIMINUI.
Ou seja, de cara, já podemos falar que a eficiência de separação que o garoto vai obter vai ser menor...
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Calcule o fator g na parede interna de uma centrífuga tubular de raio sabendo que ela gira a .
Passo 1
Lembra o que é o fator g? Ele nos indica o quanto o campo centrífugo é grande, em relação ao campo gravitacional .
Então é só aplicação de fórmula, bem de boas.
A definição do fator g é:
E só lembrando: esse termo é o campo centrífugo.
Passo 2
Nós não temos nenhuma informação sobre ou ; daí vamos ter que ir por:
Como o enunciado deu o em , vamos ter que convertê-lo para :
E cuidado com o raio! O enunciado deu diâmetro, daí tem que dividir por dois pra achar o raio:
Tanto faz a unidade que você use para o raio, mas a unidade de comprimento do raio tem que ser a mesma unidade de comprimento que aparece na gravidade. Como estou usando raio em centímetros, vou usar:
Passo 3
Agora que todas as unidades estão ok, é só jogar na fórmula:
Ou seja, o campo centrífugo na parede interna é vezes o campo gravitacional da Terra, isto é, vale na parede interna.
Resposta
Exercício Resolvido #3
UFRJ, Lista 4, Prof. Medronho
Uma centrífuga tubular de laboratório foi empregada em um teste de separação da argila contida em uma suspensão aquosa, obtendo-se um clarificado satisfatório na vazão de . Determinar a produção e o diâmetro de corte da centrífuga industrial ao operar com a mesma suspensão a .
Propriedades do fluido: e .
Passo 1
Essa questão fala de centrífugas tubulares e pede pra gente calcular vazão e para uma centrifuga industrial a partir dos dados de uma centrífuga de laboratório; ou seja, temos uma questão de mudança de escala de centrífugas. Vamos ter que trabalhar com a expressão para mudança de escala:
Usando essa expressão, conseguimos obter e . O problema pede e ; a vazão já vamos ter calculados, mas para achar , vamos ter que usar as correlações de Coelho e Massarani partindo do .
Quando estiver falando de parâmetros da escala de laboratório, vou usar o subscrito “lab” e, ao falar da industrial, “ind”.
Ahhh! Muito importante, repara que ele deu as rotações das em ; e, falando nisso, é a mesma coisa que , ok? Vamos ter que trabalhar com ela em então já vou converter logo isso, usando aquela fórmula que te mostrei lá na teoria:
Daí:
Passo 2
Para a escala de laboratório, podemos escrever:
Já para a industrial:
Fazemos a mudança de escala amarrando o diâmetro de corte, que dá no mesmo que amarrar a . Isolando-a em cada uma das equações:
Como é a mesma, podemos igualar essas duas equações (e aí dá pra cortar esse também haha ):
Queremos calcular ; isolando-o nessa expressão:
O enunciado nos deu . Embora não tenhamos os pra cada uma das centrífugas, lá da teoria (e provavelmente do seu formulário na prova haha), sabemos que para centrifugas tubulares:
Então podemos calcular e . Adotando o CGS (minha escolha) e lembrando de usar em :
Daí, calculando :
Passo 3
Pra calcular o é só pegar e substituir os valores ou pra escala de laboratório ou pra industrial. Euuuu vou pegar a escala de laboratório porque só fizemos um cálculo pra ela ( enquanto fizemos dois para a industrial então o resultado de vai estar menos suscetível a erros e aproximações. Mas, em teoria, é pra dar a mesma coisa, ok?
Como o enunciado pede o , temos que usar Coelho e Massarani. Já que temos a velocidade terminal, vamos por:
Calculando:
Antes de calcular o pela correlação, precisamos calcular e e, para isso, temos que saber a esfericidade das partículas. Como o enunciado não disse nada, vou assumir . Daí:
Usando a correlação:
Usando a definição de :
Resposta
Exercício Resolvido #4
UFRJ, Lista 4, Prof. Medronho
Uma centrífuga tubular industrial foi projetada tal que pudesse tratar de uma suspensão de amido em água a . Especifique a rotação (velocidade angular) ótima de operação da centrífuga industrial, sabendo-se que a mesma suspensão foi testada, em laboratório, em uma centrifuga tubular , tendo-se obtido um clarificado de boa qualidade a , para uma vazão de alimentação igual a . Sabe-se também que foi com base nestes dados que se projetou a centrífuga industrial.
Passo 1
Essa questão não tem nada de absurdo, mas temos que ter atenção. O enunciado pede pra calcular a rotação de uma centrífuga industrial e diz que foram feitos experimentos em laboratório; além disso, fala “Sabe-se também que foi com base nestes dados que se projetou a centrífuga industrial”; ou seja, temos uma clássica questão de mudança de escala.
E eu disse que temos que ter atenção com essa questão porque:
- Temos que trabalhar com vazões volumétricas, mas o enunciado deu a vazão mássica da centrífuga industrial, ; vamos ter que converter
- Todas as unidades têm que ser consistentes; vou escolher trabalhar no CGS então vou converter tudo que precisar para esse sistema
- As rotações que usamos nas fórmulas devem estar em
Se atentando a esses pontos, é só usar:
Lembrando que para centrífugas tubulares:
E usar para amarrar as performances das centrífugas.
Passo 2
A primeira coisa que vou fazer logo é converter a vazão mássica) da centrífuga industrial para vazão volumétrica. Sabemos que se trata de uma suspensão aquosa de amido a peso por peso. Daí, tem de amido e o resto é água.
Precisamos, agora, usar a densidade do amido e a densidade da água. Para o amido, (sim, você teria que procurar haha), e para a água à , . Sabemos que densidade é:
Daí:
E, como escolhi trabalhar com CGS, tenho que converter essa vazão aí:
Bora passar a logo pro CGS também:
E, aproveitando que estamos convertendo várias coisas, bora passar logo a rotação da centrífuga do laboratório para :
Daí:
Passo 3
Para a escala de laboratório, podemos escrever:
Já para a industrial:
Fazemos a mudança de escala amarrando o diâmetro de corte, que dá no mesmo que amarrar a . Isolando-a em cada uma das equações:
Como é a mesma, podemos igualar essas duas equações (e aí dá pra cortar esse também haha ):
Queremos calcular ; essa variável aparece em então bora, primeiro, calculá-lo; podemos isolá-lo:
Nós temos e , mas ainda não calculamos , então bora lá. Como a centrífuga é tubular:
Para :
Daí:
Para determinar , é só usar a fórmula de :
Substituindo os valores para a industrial e usando o nosso cálculo :
Já achamos o resultado, mas para treinar, bora calcular o resultado em também.
Daí: