Instalações contendo meios porosos
Produzido por Marcelo AlvesTeoria
Introdução
No tópico de escoamento em meios porosos, nós aprendemos a calcular, entre outras coisas, a queda de pressão ao passar por um meio poroso, certo? Legal, mas, na vida real, o seu desafio não vai ser apenas saber a queda de pressão em um meio poroso e sim levar água de um ponto a outro e passando por um meio poroso no meio do caminho. E aí? Como calculo isso? Bora ver?
Instalações
Nos problemas sobre instalações, vamos trabalhar, basicamente, com a equação de Bernoulli modificada e com a equação do movimento.
A equação de Bernoulli é a mesma que vemos lá em Mecânica dos fluidos:
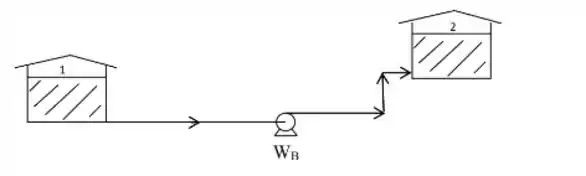
Em que:
- é a pressão no ponto
- é a velocidade no ponto
- é a altura no ponto
- é o trabalho da bomba
- é a perda de carga
Lá em mecânica dos fluidos, só víamos perda de carga por percurso na tubulação reta e por acidentes (válvulas, curvas, etc); aqui em Operações, vamos considerar também meios porosos, daí:
Podemos, ainda, escrever esse termo de perda de carga considerando um comprimento :
Em que é a soma dos comprimentos de todos os tubos retos com a soma dos comprimentos equivalentes de acidentes e de meios porosos. Caso você não lembre isso de mecânica dos fluidos, é porque ao passar por um acidente (ou meio poroso né) vai ter uma certa perda de carga; acontece que você pode dizer que essa perda de carga é EQUIVALENTE a perda que teria num comprimento de tubulação reta.

Ah! Essa equação de Bernoulli tem algumas considerações; o mais importante que você precisa saber é que ela é para fluido INCOMPRESSÍVEL, tipo água, por exemplo.
E falei que vamos usar também a equação do movimento, que é a que vimos no tópico de escoamento em meios porosos:
Perda de carga no meio poroso
Perda de carga em tubo reto e em acidentes (Exemplo: divisor de fluxo, válvula, etc) são, no geral, tabeladas. Mas a perda de carga em meio poroso não, daí vamos ter que achar uma expressão pra calculá-la.
A ideia vai ser escrever tanto a equação de Bernoulli quanto a equação do movimento para um meio poroso e achar termos iguais em cada uma delas e isolá-los e daí igualar a expressão deles. Bora ver um exemplo disso pra entender melhor?
Vamos analisar esse caso aqui, olha:
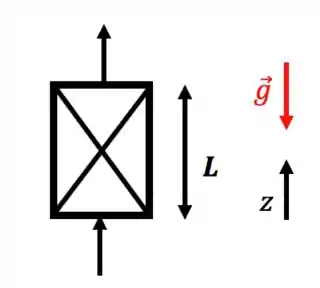
Ou seja, o fluido só está percorrendo o meio poroso e ele está indo contra a gravidade; adotei o eixo no mesmo sentido do movimento do fluido e vamos considerar o caso de fluido incompressível. Da equação do movimento, assumindo meio isotrópico e estado estacionário, temos que:
Se você tiver alguma dúvida em relação às simplificações, dá uma olhadinha no tópico anterior quando eu falo de determinação experimental de porque expliquei cada coisa que cortei lá. Continuando, podemos reescrever essa equação como:
Jogando o pra direita e integrando de até (repara que eu disse que o zero do meu eixo é onde começa o meio poroso):
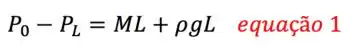
Guarda essa informação aí.
Bora ver agora como fica a equação de Bernoulli adaptada pra esse problema:
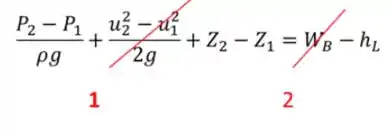
- O diâmetro por onde o fluido passa é constante daí área transversal é constante; como daí é constante
- Não tem bomba então não tem como ter trabalho da bomba né
Daí:
A diferença de alturas vale e o se resume ao , que chamei de , aí já substitui isso. O lance aqui é que o dessa fórmula é o nosso e o é o nosso . Substituindo e isolando esse termo:
![]()
E agora é a hora de juntar as duas equações. Temos, de cada fórmula, uma expressão para . Bora igualá-las:
Aparece dos dois lados; cortando, sobra:
Daqui, tiramos uma expressão para :
E guarda essa expressão para perda de carga no meio poroso com carinho. Ela é válida sempre!
Perda de carga no meio poroso
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Simplifique a equação do movimento para achar uma expressão para a queda de pressão no meio poroso em cada um dos casos abaixo:
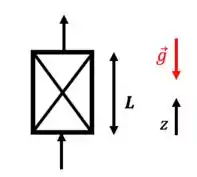
- Escoamento contra a gravidade
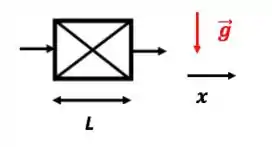
- Escoamento perpendicular à gravidade
Despreze o termo da equação do movimento!
Passo 1
Nessa questão vamos ter que manipular a equação do movimento pra achar uma expressão pro em cada um dos meios porosos apresentados. Temos o caso de uma instalação que apenas tem o meio poroso, daí a única perda que carga com a qual teremos que nos preocupar é o .
Vamos ter que usar a equação do movimento então bora logo lembrar dela:
Ah, o enunciado pede pra desprezar o termo da equação do movimento, então vou tirá-lo logo.
Ignorá-lo é uma boa aproximação... ele fica pequeno face aos outros termos.
Agora, indo pra parte que diferencia os dois casos: no primeiro caso vamos estar interessados na componente do movimento, pois é nela que o movimento se concentra, exclusivamente. Como a gravidade também se encontra nesse eixo, ela vai aparecer no equacionamento.
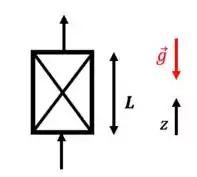
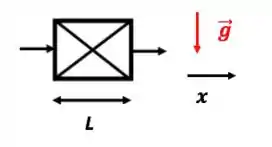
Já no segundo caso, o movimento é no eixo ; como a gravidade NÃO está presente nesse eixo, ela NÃO aparecerá no equacionamento, ou melhor, terá valor zero. Daí o termo será nulo.
Passo 2
- Escoamento contra a gravidade
- Escoamento perpendicular à gravidade
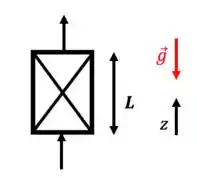
Voltando à equação do movimento, já desprezando :
Antes de continuar, mais uma simplificação: NÃO nos foram informadas variações no tempo e nem variações do espaço, daí, vamos usar as hipóteses de estado estacionário e meio isotrópico. Razoável, né?
Só há movimento no eixo z, daí vamos escrever apenas a componente dos vetores para esse eixo.
Podemos isolar o termo com nessa equação:
Jogando o pra direita e integrando de até (repara que eu disse que o zero do meu eixo é onde começa o meio poroso):
Passo 3
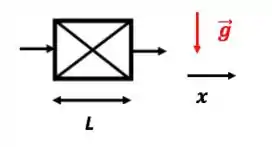
Novamente, vou usar as hipóteses de estado estacionário e meio isotrópico.
O lance é que, agora, o movimento ocorre exclusivamente ao longo do eixo x. Daí vamos escrever as componentes dos vetores apenas para esse eixo. E, como já adiantei no passo 1, a componente da gravidade nesse eixo é ZERO. Daí:
Isolando o :
Integrando, em x, de a :
Resposta
Exercício Resolvido #2
Elaboração própria
Encontre a expressão para perda de carga no meio poroso:
- Escoamento contra a gravidade
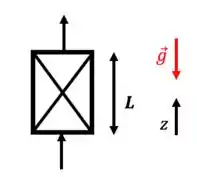
Despreze o termo da equação do movimento!
Passo 1
Como vimos na teoria, para encontrar uma expressão para perda de carga no meio poroso , precisamos usar tanto a equação do movimento como a equação de Bernoulli; encontramos um ponto de amarração, isto é, um termo igual nas duas equações e usamos ele para igualar expressões e depois isolar .
Já vimos em exercício anterior como fica o desenvolvimento da equação do movimento para esse caso:
- Escoamento contra a gravidade
Então, vou concentrar, nesse exercício, em trabalhar Bernoulli e o isolamento de .
Passo 2
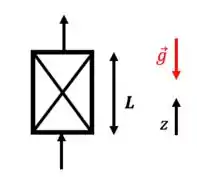
A equação do movimento simplificada para este caso é:
Indo pra Bernoulli, a equação geral é:
Repara que estou usando subscrito para o início do meio poroso e para o fim.
Podemos simplificar Bernoulli:
- O diâmetro por onde o fluido passa é constante daí área transversal é constante; como , é constante
- Não tem bomba então não tem como ter trabalho da bomba né. Daí
A diferença de alturas vale e o se resume ao , que chamei de :
Passo 2
Agora temos que juntar as duas equações:
Equação do movimento:
Bernoulli:
Substituindo a primeira na segunda:
Resposta
Exercício Resolvido #3
Elaboração própria
Encontre a expressão para perda de carga no meio poroso com escoamento perpendicular à gravidade
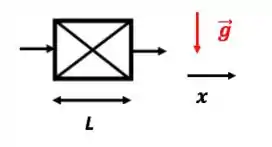
Despreze o termo da equação do movimento!
Passo 1
Como vimos na teoria, para encontrar uma expressão para perda de carga no meio poroso , precisamos usar tanto a equação do movimento como a equação de Bernoulli; encontramos um ponto de amarração, isto é, um termo igual nas duas equações e usamos ele para igualar expressões e depois isolar .
Já vimos em exercício anterior como fica o desenvolvimento da equação do movimento para esse caso:
Então, vou concentrar, nesse exercício, em trabalhar Bernoulli e o isolamento de .
Passo 2
Escoamento perpendicular à gravidade
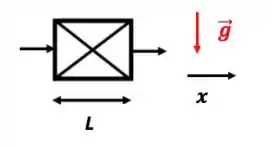
A equação do movimento simplificada para este caso é:
Indo pra Bernoulli, a equação geral é:
Repara que estou usando subscrito para o início do meio poroso e para o fim.
Podemos simplificar Bernoulli:
- O diâmetro por onde o fluido passa é constante daí área transversal é constante; como , é constante
- Não tem bomba então não tem como ter trabalho da bomba né. Daí
E mais uma coisa importante: NÃO há diferença de altura entre esses dois pontos pois o meio poroso está “deitado”. Daí:
Portanto:
E o se resume ao , que chamei de :
Passo 3
Agora temos que juntar as duas equações:
Equação do movimento:
Bernoulli:
Substituindo a primeira na segunda:
É legal lembrar do resultado com o meio poroso “em pé”, com fluxo contra a gravidade: o resultado é o mesmo!
Resposta
Exercício Resolvido #4
UFRJ, Lista 5, Prof. Medronho
Calcule a velocidade superficial de água e que passa através do meio poroso abaixo, sabendo-se que este leito foi constituído por de areia com diâmetro de . Admitir que o escoamento é darcyano.
Dados:
- Diâmetro do leito:
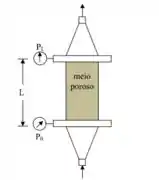
Passo 1
Essa é uma instalação bem simples: só tem o meio poroso.
Então, vamos começar caracterizando esse meio poroso, calculando e :
Para a porosidade:
Repara que usamos o SI e é fundamental que as unidades sejam iguais, para que a porosidade seja admensional!
Agora, bora calcular a permeabilidade do meio poroso :
Considerando que a areia possa ser aproximada por grãos, podemos usar . Daí:
Repara que a gente usou o diâmetro da partícula em metros, pra trabalhar no SI. A unidade que você usar no diâmetro vai definir a unidade do , já que as outras variáveis usadas são adimensionais.
Depois de achar os parâmetros do nosso meio poroso, podemos olhar pra geometria do problema e aplicar a equação de Bernoulli, já que o fluido é incompressível.
Passo 2
Aplicando a equação de Bernoulli:
Agora bora simplificar a equação, adotando o ponto como a entrada e como a saída:
- Podemos escrever a vazão como ; como vazão e área são constantes, é constante daí
- Não há bomba, daí
- , conforme vimos na teoria
Então a nossa equação simplificada ficou:
Adotando o SI:
Daí:
Como o escoamento é lento, vale a lei de Darcy:
Ainda no SI:
Resposta
Exercício Resolvido #5
UFRJ – Prof. Medronho
Estimar a capacidade, em , do filtro de areia abaixo esquematizado operando com água a . A primeira camada, com porosidade , é constituída de areia com a seguinte granulometria:
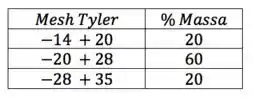
A segunda camada, como porosidade , é constituída de brita com partículas de de diâmetro. As esfericidades da areia e da brita podem ser consideradas como .
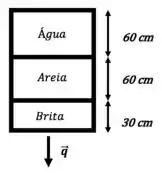
Observação: o filtro é aberto pra atmosfera tanto na entrada como na saída!
Passo 1
Vou usar subscrito para areia, para brita e chamar a água de água mesmo haha.
O enunciado dá um filtro com três camadas e pede pra calcularmos a capacidade, em , isto é, temos que calcular .
Algo importante é que sabemos (o enunciado diz) que o filtro é aberto pra atmosfera tanto na entrada como na saída, ou seja:
Passo 2
Considerando o eixo no mesmo sentido da velocidade , a equação do movimento fica:
Passando para o outro lado,
Primeiro de tudo, vamos considerar que não há perda de carga ao passar pela camada de água; isso é razoável e, de qualquer maneira, nem teríamos como estimar essa perda. Depois, vamos avaliar essa equação em cada um dos trechos.
- Para a areia:
- Para a brita:
- Para areia:
- Para a brita:
Em que:
Resolvendo a integral, temos:
Como,
Substituindo isso em , temos:
O que nos dá ! Para simplificar, vou chamar de .
Substituindo na equação 1, temos:
Sendo,
E de forma semelhante, chegamos em:
Chamei de para simplificar!
Somando as equações , eliminamos o “intermediário”, que é :
Acontece que p filtro é aberto pra atmosfera na saída, daí:
E, como desconsideramos perda de carga na camada de água, é como se fosse fluido estático, daí:
Daí:
Guarda isso por enquanto, ok?
Passo 3
Precisamos das expressões do . Como enunciado NÃO fala que escoamento é lento, usamos Forchheimer:
Epa! Não temos ; temos que determiná-los. Como não temos experimentos, usamos as correlações.
Para :
Repara que é o diâmetro médio de Sauter e foi calculado com os dados daquela tabelinha que o enunciado deu.
Para calcular , usamos a correlação de Santana e Massarani:
Em que e essa correlação é válida para valores de entre:
Daí:
Substituindo os nas expressões de e substituindo essas na equação que pedi pra você guardar:
Resolvendo a equação de segundo grau gerada:
A segunda opção NÃO tem sentido físico. Sabemos que o fluido tem que descer, por causa da gravidade, e dissemos que o sentido positivo do eixo z é para baixo, daí tem que ser positivo. Daí:
Como o enunciado pede nas unidades , convertemos e: