Escoamento em meios porosos
Produzido por Marcelo AlvesTeoria
Introdução
Antes de começar a ver as equações para meios porosos, queria revisar dois operadores com você, porque vamos precisar bastante deles. São eles: gradiente e divergente.
- Operador gradiente: aplicamos em um escalar e obtemos como resultado um vetor. Considerando eixos cartesianos e usando a temperatura como exemplo , ele fica:
Em que são os vetores unitários de cada eixo.
Aplicando o gradiente em uma propriedade, obtemos a informação de como essa propriedade varia no espaço, em cada um dos eixos.
- Operador divergente: aplicamos em um vetor e obtemos um escalar. Usando a velocidade como exemplo e considerando eixos cartesianos:
Em que são as componentes da velocidade, respectivamente.
E ah! Repara que tem um pontinho entre , que simboliza o produto escalar.
Equações da continuidade e Movimento
Lá da mecânica dos fluidos, podemos escrever equação da continuidade (é um balanço de massa) e equação do movimento (é um balanço de forças) para o FLUIDO.
Em que:
Mas temos um problema: o meio poroso é todo louco, sem nenhuma simetria; o fluido vai indo por vários poros diferentes e aleatórios. Além disso, definir a velocidade ponto a ponto seria quase impossível, assim como definir as paredes. Precisamos achar outro jeito de continuar nosso desenvolvimento pra meios porosos.
Teoria das misturas da mecânica do contínuo
A solução é simples até: vamos reescrever essas equações, mas, agora, considerando não só o fluido mas sim FLUIDO E SÓLIDO, em uma proporção igual à porosidade . Tipo, se consideramos um balanço pegando de fluido e de sólido. As equações ficam:
Em que:
Daí, é a reação que a matriz faz no fluido. E repara que escrevemos a equação do movimento considerando apenas as forças que atuam no fluido.
Mas ainda temos o problema de não conseguir definir ponto a ponto...e não tem muito o que fazer não; vamos adotar a estratégia de perder esse detalhamento pra conseguir resolver. Vamos definir uma velocidade superficial , considerando a área da do tubo (ou outro lugar) em que o meio poroso está inserido;
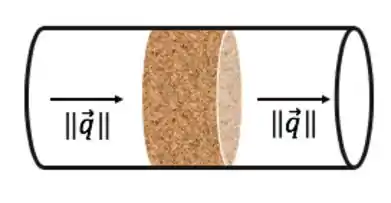
O módulo de vale:
Em que:
é como se fosse a velocidade antes e depois do meio poroso. Por isso ele recebe esse nome de “velocidade superficial”. O fluido tem essa velocidade até a superfície do meio poroso. É uma condição de contorno. Podemos relacioná-la com da seguinte maneira:
Juntando as duas expressões:
Daí:
Com base em , as equações ficam:
E são essas equações que vamos, efetivamente, usar.
Equações para
Até agora sabemos da existência de uma forca entre líquido e sólido (força ), mas não conhecemos fórmulas pra ela. Bora ver duas correlações empíricas:
- Correlação de Forchheimer
Vou começar da correlação mais geral, ok? Para meio isotrópico (quando as propriedades físicas não variam com a posição), Forchheimer diz que:
Em que
Sendo que
Em que é o Reynolds do meio poroso.
E falando em permeabilidade, deixa eu apresentar logo pra você uma unidade “especial”, que é o Darcy .
- “Lei” de Darcy
A lei de Darcy é um caso especial da correlação que a gente acabou de ver, mas para situações onde (além do meio isotrópico e fluido Newtoniano) estamos falando de escoamento lento, com Reynolds baixo. Mais precisamente, a lei de Darcy é válida quando:
E a “lei” fica com essa carinha:
Determinação experimental de e
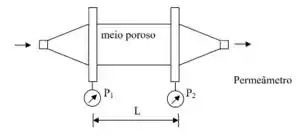
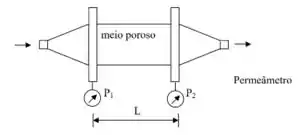
Para a determinação experimental de e , usamos um permeâmetro; nada mais é do que um tubo contendo o meio poroso; variamos a vazão de um fluido que passa pelo meio poroso e anotamos a queda de pressão do fluido ao passar pelo meio poroso (MP) com essa tal vazão. Para isso, medimos a pressão antes e depois do meio poroso, né.
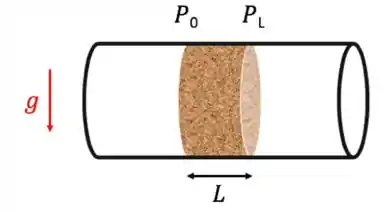
Como ao escoar pelo meio poroso o fluido perde carga:
Depois de fazer os experimentos e ter uma tabelinha relacionando e , vamos usar a equação do movimento para determinar e . Acontece que o fluido pode ser incompressível ou compressível e o escoamento pode ser lento (darcyano) ou um escoamento qualquer (aí usa Forchheimer para ). Vou te mostrar agora como trabalhar com cada um desses casos; em todos eles, vamos assumir:
- Fluido Newtoniano
- Escoamento unidimensional, permanente (estado estacionário) e isotérmico
- Meio poroso isotérmico (Temperatura constante)
- Escoamento de fluido incompressível
- Em estado permanente não há variação no tempo
- Gradiente nos diz como uma propriedade varia no espaço; assumimos meio poroso isotrópico daí NÃO há variação no espaço
- Não está listado nas hipóteses, mas vamos assumir que as forças viscosas são desprezíveis face a
- O escoamento é na horizontal e a gravidade está na vertical. É importante lembrar que isso é para ESSE exemplo que eu estou desenvolvendo com você, ok? Se o escoamento fosse na mesma direção que a gravidade, ia ter que considerar esse termo!
- Escoamento Darcyano (lento)
- Escoamento qualquer
- Escoamento compressível
Vamos pegar a equação do movimento e fazer as simplificações que der:
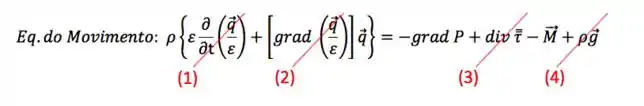
Depois das simplificações, só sobra:
Mas assumimos escoamento unidimensional, lembra? Chamando o eixo da direção do escoamento de , o gradiente se resume a . Daí:
Mas esse escoamento incompressível pode ser lento (darcyano) ou um escoamento qualquer; bora ver cada caso:
Se o escoamento é Darcyano, vale:
Daí, voltando na equação do movimento com as simplificações:
Separando as variáveis e integrando do inicio ao fim do meio poroso, chamando o módulo de de :
Repara que e saíram da integral porque são constantes; é constante porque assumimos isotérmico, é constante porque assumimos isotrópico e é constante porque a área transversal do meio poroso é constante.
Resolvendo a integral:
Fazendo , ou seja, maior menos menor, e rearranjando:
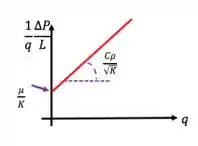
Isso é uma reta! Tendo os pontos relacionando e (conseguimos tirar a partir de ), podemos fazer regressão linear:
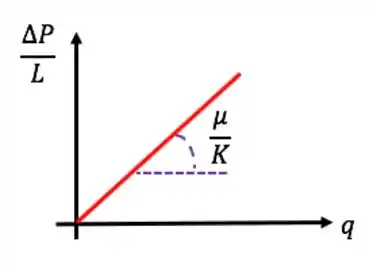
Quando não pudermos assumir escoamento darcyano, temos que usar Forchheimer para :
Daí a equação do movimento com as simplificações e já integrada fica:
Dividindo tudo por e simplificando o termo mais à direita:
E adivinha o que isso é: uma reta! Dá pra fazer, também, regressão linear com os dados:
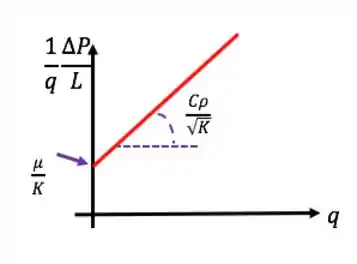
Repara que nesse caso a reta tem um coeficiente linear diferente de zero.
Quando o escoamento é compressível, ao mudar a pressão altera-se a vazão volumétrica; como:
Ao alterar a vazão volumétrica, alteramos o módulo de . Aí, seria mais complicado integrar porque teríamos que saber a relação de com . Masssss, embora haja alteração no volume, a massa não se altera né. Daí vamos usar uma estratégia ao trabalhar com escoamento compressível, que vai ser multiplicar a equação pela densidade .
Como usamos as mesmas simplificações seja o escoamento incompressível ou compressível, chegamos, também, em:
- Escoamento Darcyano
- Escoamento qualquer
Temos que multiplicar tudo por . Disso, surge uma definição:
Também podemos escrever como:
Em que é a vazão mássica.
Voltando àquela equação a ser integrada e fazendo separação de variáveis, depois de multiplicá-la por :
A questão é que densidade é massa por volume e, como o volume está variando, a densidade NÃO é constante. Assumindo gás ideal e rearranjando , chegamos a:
Em que é o peso molecular médio. Substituindo isso na integral:
Posso reescrever isso como:
O termo entre colchetes é uma densidade média, , calculada entre .
E essa é a nossa equação de trabalho para escoamento compressível Darcyano. Adivinha: é uma reta haha. Depois de experimentos, podemos fazer regressão linear para determinar .
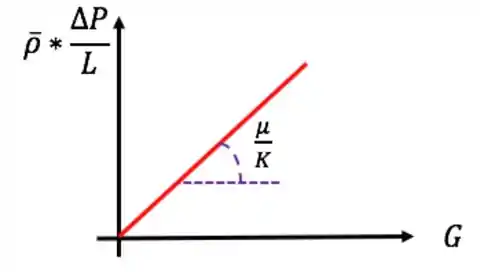
Podemos seguir a mesma ideia e fazer o desenvolvimento pra um escoamento qualquer, em que temos que considerar Forchheimer:
Já vou colocar o resultado final, ok?
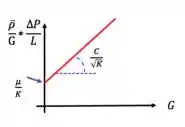
Isso também é uma reta e podemos fazer regressão linear:
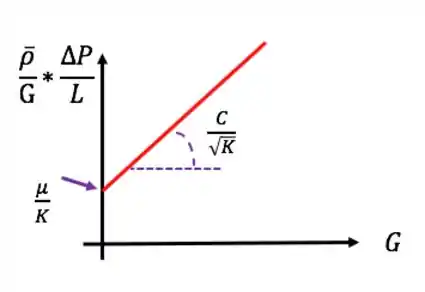
Estimativa de e
Quando não temos dados experimentais, podemos fazer uma estimativa de e por correlações. Para , temos o modelo de Kozeny-Carmán:
Em que (esfericidade) e (diâmetro médio de Sauter) são relativos às partículas que compõem o meio poroso. Quanto ao , este é um fator de correção (também relativo às partículas que compõem o meio poroso) cujo valor está entre . Os extremos são:
Provavelmente, você só vai ter que trabalhar com os valores extremos.
Para , temos a correlação de Costa e Massarani:
Em que .
Teoria das misturas da mecânica do contínuo
Equações para M →
Determinação experimental de K e C
Estimativa de K e C
Exercícios Resolvidos
Exercício Resolvido #1
Massarani, G. (2002), Fluidodinâmica em Sistemas Particulados, 2 ° e d
Estimar os valores de e pelas correlações da literatura. Considerar que a esfericidade da areia é .
Meio de areia
- Granulometria da areia:
- Porosidade do meio:
Passo 1
Nessa questão, é só aplicar as correlações pra estimar e . Para , temos o modelo de Kozeny-Carmán:
Em que (esfericidade) e (diâmetro médio de Sauter) são relativos às partículas que compõem o meio poroso. Quanto ao , este é um fator de correção (também relativo às partículas que compõem o meio poroso) cujo valor está entre e. Os extremos são:
Como a areia NÃO possui esfericidade igual a 1, vamos usar .
Repara que o enunciado não deu o diâmetro médio de Sauter direto, mas deu a faixa Mesh Tyler da areia; daí, usamos a tabela pra passar esses valores de Mesh para centímetros e depois calculamos o diâmetro médio.
A fórmula de diâmetro médio de Sauter considerando porcentagem de massa de partículas entre dois é:
Como só há um intervalo, a fórmula se resume à média aritmética:
Já para , temos a correlação de Santana e Massarani:
Em que e essa correlação é válida para valores de entre:
Passo 2
Calculando :
Repara que esse valor está na faixa de validade da correlação de ; bora calculá-lo:
Resposta
Exercício Resolvido #2
Massarani, G. (2002), Fluidodinâmica em Sistemas Particulados, 2 ° e d
Determinar os valores da permeabilidade e do fator a partir dos dados experimentais obtidos por permeametria.
Meio de areia artificialmente consolidado com de araldite.
- Granulometria da areia:
- Fluido: água
- Comprimento do meio:
- Área da seção de escoamento:
- Porosidade do meio:
- Dados de velocidade superficial e queda de pressão:
![]()
Passo 1
O enunciado nos deu dados experimentais de e pediu pra calcularmos COM BASE NOS DADOS EXPERIMENTAIS os valores de (permeabilidade) e (fator sem nome).
Como vamos ter que usar os dados experimentais, temos que partir da equação do movimento para relacionar e ; esse desenvolvimento eu já fiz pra você lá na teoria, então vou pular, ok? Só temos que identificar qual caso aplicar.
Já que o fluido é água, podemos assumir fluido incompressível; e como o enunciado NÃO fala que o escoamento é lento, NÃO podemos assumir isso e, por isso, usamos a equação de Forchheimer para . Daí vale:
Depois de identificado o caso, é só fazer regressão linear com os dados:
Temos que nos atentar se estamos usando tudo no mesmo sistema de unidades; vou adotar o CGS, daí vou converter logo e . No caso do , vou primeiro chegar numa expressão geral pra conversão e depois converto todos.
Daí, em :
![]()
Ah! Na teoria, eu defini e, dessa forma, fica positivo. Nessa questão, ele definiu de forma que ficava negativa e por isso colocou um menos na tabela, pra deixar positivo; então definiu . Daí o da tabela original é o mesmo que o meu .
Passo 2
Agora é só fazer a regressão linear com os dados fornecidos; comparando a equação de trabalho com a equação de uma reta:
Temos que:
Adicionando uma linha para na nossa tabela e usando :

Fazendo a regressão linear :
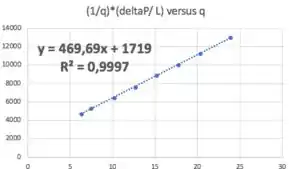
Daí:
Na primeira equação não conhecemos duas variáveis; na segunda, uma. Então começamos pela segunda.
Da primeira:
Repara que nem usamos algumas informações.
Resposta
Exercício Resolvido #3
Massarani, G. (2002), Fluidodinâmica em Sistemas Particulados, 2 ° e d
Determinar os valores da permeabilidade e do fator a partir dos dados experimentais obtidos por permeametria.
Meio não consolidado de areia
- Granulometria da areia:
- Fluido: ar a e pressão atmosférica na descarga
- Comprimento do meio:
- Área da seção de escoamento:
- Porosidade do meio:
- Dados de velocidade mássica e queda de pressão:
![]()
Passo 1
O enunciado nos deu dados experimentais de e pediu pra calcularmos COM BASE NOS DADOS EXPERIMENTAIS os valores de (permeabilidade) e (fator sem nome).
Como vamos ter que usar os dados experimentais, temos que partir da equação do movimento para relacionar e ; esse desenvolvimento eu já fiz pra você lá na teoria, então vou pular, ok? Só temos que identificar qual caso aplicar.
Como o fluido é ar, o fluido é compressível; e como o enunciado NÃO fala que o escoamento é lento, NÃO podemos assumir isso e, por isso, usamos a equação de Forchheimer para . Daí vale:
Depois de identificado o caso, é só fazer regressão linear com os dados:
Temos que nos atentar se estamos usando tudo no mesmo sistema de unidades; vou adotar o CGS; cuidado com a unidade desse aí porque ela pode confundir. Embora tenha um na unidade, NÃO está no CGS; pra pressão, a unidade do CGS é . Daí vou converter logo ; vou primeiro chegar numa expressão geral pra conversão e depois converto todos.
![]()
Massss, para fluido compressível, não basta saber o ; como temos que calcular , já que ele aparece na fórmula a se fazer regressão linear, e a fórmula dele é:
Precisamos de . O segundo já foi dado, só precisamos passar pro CGS:
Já , como:
Calculando em cada ponto:

Passo 2
Antes de fazermos a regressão linear, precisamos calcular para cada caso.
Para calcular ,precisamos da temperatura em escala absoluta; vou passa-la pra Kelvin.
Como estamos trabalhando no CGS, usamos:
Por se tratar de ar atmosférico, . Daí:

Passo 3
Agora que temos tudo que precisamos, podemos fazer a regressão linear:
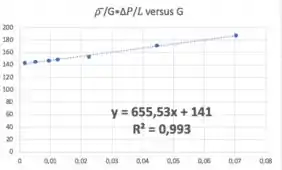
Comparando a equação de trabalho com a equação de uma reta, :
Daí:
Antes de continuarmos, precisamos do . Indo atrás de algum valor tabelado, achamos que para o ar nas condições do problema, . Daí:
Da outra equação:
Resposta
Exercício Resolvido #4
Determine a queda de pressão no reator catalítico de leito fixo sabendo-se que este opera isotermicamente a e que a pressão na descarga é de .
Dados:
- Vazão mássica de gás (propriedades do ):
- O catalisador forma um leito de de diâmetro e de altura, com porosidade
- As partículas seguem a distribuição CGS de parâmetros e
- A esfericidade das partículas é
Passo 1
Primeiro, vou calcular o diâmetro médio de Sauter porque vamos precisar dele para calcular . Foi dado que:
Daí:
Lá do tópico de diâmetro médio, sabemos que uma das formas de o calcular é:
Usando o modelo de Kozeny-Carmán para e adotando o sistema de unidades CGS:
Usando a correlação de Massarani para :
Em que e essa correlação é válida para valores de entre:
Daí:
Passo 2
Aplicando a equação do movimento:
Supondo estado estacionário, meio isotrópico e que forças viscosas são desprezíveis face à :
Repara na física do problema que só tem variação de pressão em ; numa mesma altura a pressão vai ser constante.
Vamos ter que usar aquele artifício de multiplicar tudo por para aparecer o :
Daí a equação fica:
Repara que considerei fluxo de massa indo contra a gravidade e já mexi com os sinais.
Como o enunciado NÃO fala que escoamento é lento, usamos Forchheimer:
Substituindo isso na equação:
Guarda isso aí.
Passo 3
Considerando gás ideal:
Substituindo isso naquela equação do passo anterior e integrando:
Como a temperatura é alta e a pressão NÃO é muito alta, a densidade vai ser bem baixa e por isso vou desprezar esse último termo da direita. Daí sobra:
Que é a mesma fórmula que chegamos pra escoamento horizontal.
Bora calcular logo o :
O enunciado deu que . Vou escolher trabalhar no SI então vou ter que passar esse por hora pra por segundo.
Já o :
Sabemos que a pressão na descarga é ; no SI, .
Além disso, . Daí
Substituindo tudo naquela equação integrada:
Repara que joguei tudo no SI. E o eu procurei em tabela de livro.
Essa equação aí em cima cai numa equação do segundo grau e os resultados são:
Escrevemos o como maior menos menor daí ele é escrito de forma a ser positiva! Daí: