Balanços de Energia e Tamanho do Flash
Produzido por Marcelo AlvesTeoria
Balanço de Massa e Energia
Beleza, até agora já sabemos o que é o flash, o que fazemos com ele, como fazer algumas contas... mas ainda não falamos de balanço de energia dentro do flash. E isso é muito importante quando queremos achar a temperatura da carga de um flash térmico, por exemplo.
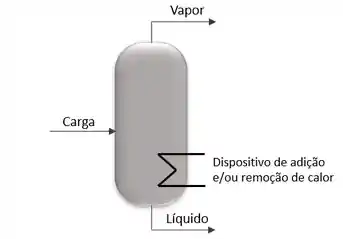
Obs: isso não significa que não podemos ter balanço de energia no flash mecânico, ok?
Para a gente começar, vamos relembrar as equações que já vimos de balanço de massa para o nosso flash.
Sabemos que tudo que entra é igual a tudo que sai, então:
E podemos representar isso também em função das composições:
Agora, vamos pegar a nossa primeira equação de balanço de massa e pensar nela em termos de energia? A gente tem a “energia” da corrente de carga e a do dispositivo de entrada de calor (obs: estamos considerando que ele acrescenta calor) entrando no sistema. E, saindo do sistema, temos a energia das correntes de líquido e vapor. Vamos representar a energia através da entalpia “”, ok?
Para os casos das correntes que tem massa entrando e saindo, ou seja, todas elas que aparecem no balanço de massa, precisamos multiplicar a energia pela vazão dessas correntes. No caso do , que é o calor do dispositivo, ele nem aparece no balanço de massa, pois nele só há troca de energia. Então não precisamos multiplicar por nenhuma vazão, pois essa vazão não existe! Caso o dispositivo esteja removendo calor, ao invés de adicionar, basta mudar o sinal dele, ok?
Podemos reorganizar nosso balanço de energia para aparecer o nosso famoso , que representa a fração vaporizada! Dividindo tudo por :
Como:
Obtemos que:
E vamos introduzir uma nova variável, o
Então:
E a última equação que nunca podemos esquecer resolvendo essas questões é:
Tipos de Problemas
Beleza, talvez você esteja se perguntando como isso pode cair na sua prova. Nós temos uma previsão dos problemas de balanço de energia que podem aparecer. Se liga aí:
1. e conhecidos
2. e conhecidos
3. e conhecidos
4. e conhecidos
5. e conhecidos (quase nunca aparece!!!!)
Vamos agora olhar cada um dos principais casos para vermos qual seria o esquema para resolver cada um deles, ok?
Antes de mais nada, vamos combinar uma numeração para as equações que vamos usar para ficar mais fácil de montarmos o esquema de resolução de cada um dos casos!
Equação 01:
Equação 02:
Equação 03:
Equação 04:
Observação: dependendo da questão, a entalpia da fase líquida e da fase vapor pode não ser dada diretamente... Então vou te mostrar como calcular elas, ok? Vamos chamar de “Conjunto de Equações 05”.
Tipos de Problemas: Caso 01
Nesse tipo de problema, e são especificados. E o procedimento que temos que seguir é o seguinte:
Equação 01 Determinar o
Equação 02 Determinar o e o
Conjunto de Equações 05 Determinar e
Tipos de Problemas: Caso 02
Nesse tipo de problema, e são conhecidos e a ordem que vamos usar as equações vai ser:
Equação 01 Determinar pressão
Se você olhou para a equação 01 e não viu nada de pressão lá, calma! Nela a gente tem o . E uma das formas de escrever é:
Então a pressão tá “escondida” dentro do !
Equação 02 Determinar o e o
Conjunto de Equações 05 Determinar e
Equação 03 Determinar o
Tipos de Problemas: Caso 03
Nesse tipo de problema, e são conhecidos. A “rotina” que vamos seguir nesse caso será:
Equação 01 Determinar temperatura
Novamente, a temperatura também está escondida dentro do
Equação 02 Determinar o e o
Conjunto de Equações 05 Determinar e
Equação 03 Determinar o
Tipos de Problemas: Caso 04
Nesse tipo de problema, e são conhecidos, e a ordem que vamos usar as equações vai ser:
Estimar temperatura
Equação 01 Determinar
Como temos um valor de temperatura e sabemos a pressão, vamos aplicar a Equação 01 para determinar .
Equação 02 Determinar o e o
Conjunto de Equações 05 Determinar e
Equação 03 Determinar o
Comparar o calculado com o valor dado. Caso seja próximo, questão finalizada. Caso não seja próximo, precisamos chutar uma nova temperatura!
Tipos de Problemas: Caso 05
É muito pouco provável que esse tipo de problema apareça na sua prova. Portanto, nem vamos incluir a rotina para cálculo dele aqui, tá bom?

Determinação do Tamanho do Flash
Agora que já vimos várias possibilidades de contas para o flash, bora aprender a dimensionar o nosso equipamento de flash?
Para tanques verticais, o tamanho do vaso de flash será uma função da composição e da vazão dos produtos de topo (vapor) e fundo (líquido).
Vamos considerar que o nosso tanque flash admite uma velocidade máxima, . Essa velocidade foi determinada empiricamente como:
Sendo que as precisam estar em e a constante do tanque () é dada pela seguinte fórmula:
E esse ? é dado em função das vazões mássicas ( e , das correntes de líquido e vapor.
E são as nossas constantes:
OBS: Sempre que calcular o ,confere se ele ficou entre e , pois esse é o intervalo em que essa fórmula é válida.
Podemos relacionar a vazão molar da fase vapor com a velocidade, área transversal e outros parâmetros, conforme equação abaixo:
Onde é a área transversal do nosso tanque e é a massa molar média da fase vapor. Com isso, conseguimos achar essa área transversal, e, a partir dela, achar o diâmetro.
FECHOU!!! Agora já sabemos até dimensionar o flash. Corre lá para os exercícios para aplicarmos tudo isso 😊

Tipos de Problemas
Tipos de Problemas: Caso 01
Tipos de Problemas: Caso 02
Tipos de Problemas: Caso 03
Tipos de Problemas: Caso 04
Tipos de Problemas: Caso 05
Determinação do Tamanho do Flash
Exercícios Resolvidos
Exercício Resolvido #1
Prova Cesgranrio – 2011 – Petrobras -Engenheiro de Processamento Júnior
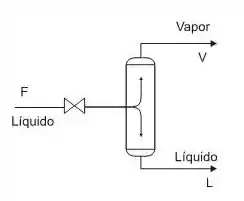
A figura acima representa um flash adiabático de uma mistura líquida que passa por uma válvula de controle de pressão do vaso para garantir vaporização parcial da mistura. Considerando-se que a válvula está muito próxima ao vaso e desprezando-se a perda de carga na tubulação, é INCORRETO afirmar que a(o):
- Temperatura após a válvula será sempre inferior à temperatura antes da válvula.
- Razão V/L após a válvula será igual à razão V/L obtida na saída do vaso.
- Vazão de carga F, se aumentar, mantendo-se a pressão no vaso, mudará a razão V/L obtida anteriormente.
- Vapor será formado por expansão da mistura líquida que sai da válvula, quando essa mistura entra no vaso.
- Balanço de energia no sistema global é dado pela equação: , desprezando-se a variação de energia cinética antes e após a válvula.
Passo 1
Vamos avaliar letra por letra para resolver essa questão, beleza?
Mas antes disso vamos falar um pouco sobre o flash adiabático. Nesse tipo de flash, não temos um dispositivo de aquecimento/resfriamento. O que temos é uma válvula que será responsável por controlar a pressão e provocar uma despressurização rápida. Nessa despressurização rápida, parte da amostra vai se volatilizar. É o nosso bom e velho flash mecânico, que é “adiabático” porque não troca calor com o ambiente.
Passo 2
Vamos avaliar a letra a) então!
Na letra a), está escrito que a temperatura após a válvula é inferior a temperatura antes da válvula. Isso é verdade pois, em despressurizações, a pressão cai e a temperatura cai também.
Uma forma de ver isso é a gente lembrar da lei dos gases ideais:
Para volume constante, se a pressão diminui, a temperatura precisa diminuir também!
Passo 3
Na letra b), está dizendo que a razão entre a vazão de vapor e líquido após a válvula e na saída do vaso são iguais.
Isso é verdade, pois é a válvula que promove a vaporização. Então, depois disso, nada mais vai virar vapor, e, portanto, nem a vazão de vapor nem a de líquido irão variar mais.
Passo 4
Para a letra c), temos que: “Vazão de carga F, se aumentar, mantendo-se a pressão no vaso, mudará a razão V/L obtida anteriormente.”
Bem, isso faz sentido, pois temos uma vazão maior e a operação está ocorrendo na mesma pressão. Logo, a porcentagem que será vaporizada mudará. Com isso, a razão não se mantém. Assim, a afirmativa c é verdadeira.
Passo 5
A letra d) diz que “Vapor será formado por expansão da mistura líquida que sai da válvula, quando essa mistura entra no vaso”. Essa afirmativa está errada, pois da saída da válvula já sai a mistura líquido e vapor, e no vaso eles apenas se separam 😊

Portanto, essa é a nossa resposta... Mas, vamos avaliar a letra e) também.
Passo 6
A letra e) se refere ao balanço de energia que vimos nesse tópico, né? E ele tá certinho....
Tá considerando as entalpias de todas as correntes que entram, ponderadas pela vazão, e das que saem também... Como não tem dispositivo de trocar de calor, o nosso desaparece!
Resposta
Letra d)
Exercício Resolvido #2
Lista 1 - Operações Unitárias II – UFRJ. Modificada.
Uma mistura binária equimolar n-heptano/n-octano é submetida a um flash a 1 atm em que 60% da alimentação é vaporizada. Determine:
a) Composições dos produtos vapor e líquido.
b) Temperatura da solução antes da válvula de redução de pressão.
Dados:

Passo 1
Primeira coisa que precisamos fazer é entender de qual tipo de flash o equipamento está falando!
Nesse caso, o enunciado fala para gente de uma válvula de redução de pressão. Então, a gente tá falando de flash mecânico. Beleza?
E aí vamos aos poucos determinar o que a questão tá pedindo, beleza?
Passo 2
Se está dizendo que é uma mistura binária equimolar, já sabemos os valores de (da carga) para ela.
Em que nC7 representa o n-heptano e nC8, o n-octano.
A questão quer saber as composições dos produtos de topo e fundo (vapor e líquido, respectivamente).
Então isso remete a gente às simplificações que já conhecemos de ponto de bolha e ponto de orvalho para cada um. No entanto, a composição que conhecemos é da carga e não dos produtos líquido e vapor. Logo, não podemos ir direto para essas equações.
A primeira coisa que precisamos fazer é aplicar a equação de flash para o nosso tanque para conseguirmos descobrir a temperatura dele. Beleza?
Então, falou de precisamos lembrar que:
E é dado pela equação de Antoine.
Nossa equação completa para dois componentes fica assim:
Então, vamos buscar os dados que faltam na nossa tabela. Atenção para as unidades da temperatura e pressão de acordo com a tabela que você usar, beleza? Também tem que ficar ligado se a equação de Antoine tá como “log” ou “ln”. Pra equação no formato que estamos usando aqui e com as devidas unidades, vamos ter:

Bora substituir tudo na nossa equação?
Lembrando que o foi dado igual a 0,6 quando ununciao nos diz que temos 60% de vaporização da carga!
Como resultado para temperatura, obtemos que:
Nem pensa em resolver essa equação na mão. Usa sua calculadora e já grava essa equação lá!
Passo 3
Achamos a temperatura do tanque de flash e, com isso, vamos obter a composição do nosso vapor e do líquido. Mas, como?!?!
Bem, com essa temperatura vamos começar calculando os . A partir deles, vamos achar os e .
Aplicando para cada um dos nossos compostos, temos que:
Passo 4
Agora que conhecemos os , vamos achar os e
Então para cada um dos componentes, vamos encontrar os ...
Como , podemos achar nossos :
Passo 5
Com isso, fechamos a primeira parte. A segunda coisa que precisamos calcular é a temperatura antes da válvula de redução de pressão.
Para isso, vamos precisar usar os balanços de energia que vimos e as informações que já calculamos até agora.
Onde:
Primeira coisa para facilitar nossa vida, repara que na parte do aparece uma . Essa temperatura de referência é arbitrária, ou seja, nós podemos escolher!
Para ficar mais fácil nosso problema vamos falar que:
Assim, nosso . Por consequência, , pois todas suas parcelas dependem de , que é nulo.
Além disso, como estamos falando de um flash mecânico, não há dispositivo para adicionar ou remover calor. Dessa forma, .
Logo, nosso balanço de energia pode ser reescrito como:
Passo 6
Vamos calcular, então, cada uma dessas entalpias.
é um líquido. Portanto, podemos calcular sua entalpia por:
Pelos dados lááá da tabela do enunciado:
Para o , podemos simplificar a equação:
Para:
Já que na temperatura de referência que escolhemos .
Portanto, mais uma vez usando a tabela do enunciado, temos que:
Substituindo tudo no nosso balanço de energia, conseguimos achar a temperatura da carga (que é a temperatura antes da válvula).
Portanto:
Resposta
Exercício Resolvido #3
Elaboração própria
Considere uma separação binária de A e B através de um flash. Calcule o valor da fração vaporizada.
Dado: , e
Passo 1
A questão nos pede para calcular o valor da fração vaporizada, ou seja, o nosso . Para isso nos forneceu os valores de e . Então precisamos encontrar equações que relacionem as nossas incógnitas, beleza?
Passo 2
Vimos na teoria a seguinte expressão:
Em função do componente A ficamos com:
Repara que dessa equação nós só temos o , precisamos ainda achar , mas para encontrar o valor de precisamos ainda encontrar a constante de equilíbrio de A (, então vamos lá, uma coisa de cada vez.
Passo 3
Para calcular a constante de equilíbrio nós vimos na teoria a seguinte expressão:
Colocando, também, em função do componente A ficamos com:
Como já temos os valores de e , basta substituir, uhuuuull! E ficamos com:
Passo 4
Agora, finalmente, podemos voltar a equação inicial:
Pois já temos , que foi dado e e , que foram calculados. Substituindo os valores vamos ficar com:
Fazendo as contas encontramos o . Ou seja, temos de fração vaporizada😉.
Resposta
Exercício Resolvido #4
Caderno Operações Unitárias II - UFRJ
Uma mistura de de , de e de é sujeita a separação por flash a uma pressão de , onde da carga é vaporizada.
Determine a Temperatura do Tanque de Flash, a composição dos produtos e Temperatura da Carga.
Dados:
Equação de Antoine

Calores específicos e ( entalpia de vaporização)- Valores médios entre

Passo 1
Primeira coisa que podemos fazer é identificar o tipo de problema para saber qual passo a passo iremos seguir, ok?
Nós conhecemos a pressão e sabemos também a porcentagem vaporizada (). Portanto, esse é um problema do tipo 3. E usaremos a sequência para problemas desse tipo para resolvê-lo, igualzinho a que vimos na teoria, ok?
Passo 2
Bem, a primeira coisa que precisamos calcular então é a temperatura do nosso tanque de flash.
Para isso, vamos partir da equação de Flash:
Lembrando que :
Portanto, nossa equação de Flash fica com essa carinha aqui:
Substituindo as constantes e os valores de , temos que:
E aí coloca sua calculadora que faz iteração para trabalhar e a temperatura que ela vai achar vai ser:
DICA:Se por acaso a sua calculadora não tiver essa função, um bom chute para essa temperatura é:
Mas assim, não vai dar o mesmo resultado... Nesse caso, se você tentar deve encontrar , mas é melhor que nada :P
Passo 3
Já achamos a temperatura! Agora, que temos a temperatura, conseguimos calcular o e, em consequência, e .
Portanto, vamos substituir:
Em seguida, vamos encontrar o .
Substituindo:
Como , nosso .
Passo 4
Para encerrar essa questão, precisamos de calcular a temperatura da carga. Como a carga é a temperatura da entrada no processo, e não de uma saída, não podemos usar as equações de Flash, Bolha ou orvalho. Precisamos fazer o balanço de energia!
Nesse caso, não foi falado nada sobre o dispositivo de adição/ remoção de calor, então vamos considerar
Onde:
Como essa temperatura de referência é arbitrária, para ficar mais fácil nosso problema vamos falar que:
Assim, nosso . Por consequência, , pois todas suas parcelas dependem de , que é nulo.
Logo, nosso balanço de energia pode ser reescrito como:
Passo 5
Vamos calcular então cada uma dessas entalpias. é um líquido, portanto, podemos calcular sua entalpia por:
Para o , podemos simplificar a equação para
, uma vez que na temperatura de referência que escolhemos .
Portanto, temos que
Substituindo tudo na nossa fórmula conseguimos achar a temperatura da carga.
Resposta
Exercício Resolvido #5
Elaboração própria
Sabendo que temos um equipamento flash, como o da imagem abaixo. Deduza o balanço de energia para um dispositivo removedor de calor.
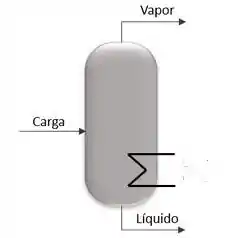
Passo 1
A questão nos pede para deduzir o balanço de energia para o flash no caso de um dispositivo removedor de calor. Então será similar a teoria, onde ao invés de adicionar, o dispositivo vai estar removendo calor.
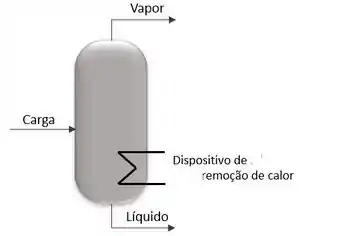
Passo 2
Primeiro nós vamos fazer o balanço de massa, lembrando que tudo o que entra é igual ao que sai, beleza? Então ficamos com:
E colocando em função das composições vamos ter:
Show! Repara que o balanço de massa vai ser o mesmo para o flash com o dispositivo tanto removendo como adicionando calor, pois estamos trabalhando até então APENAS em função massa. Bora ver como seria o nosso balanço de energia então?
Passo 3
Para o balanço de energia nós vamos ter a “energia” da corrente de carga entrando no sistema. Já saindo do sistema, temos a energia das correntes de líquido, vapor e a do dispositivo de remoção de calor. Como representamos a energia através da entalpia “”, ficamos com:
Reorganizando nosso balanço de energia para aparecer o , que representa a fração vaporizada, temos:
Como e , obtemos que:
E o , então: