Equação de Flash
Teoria
Equipamento Flash
Nós já vimos que existe um equipamento chamado flash e que ele pode ser ou térmico ou mecânico. No flash térmico, a gente vai ter uma variação de temperaura, provocada por um dispositivo de adição e/ou remoção de calor, que vai promover a separação. Já no flash mecânico, a gente vai ter uma válvula que vai provocar uma variação de pressão e, assim, promover a separação. Beleza?
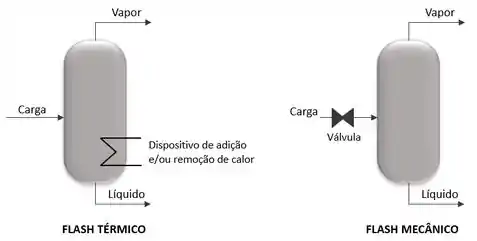
Portanto, esses vão ser os equipamentos (flash mecânico e térmico) que traduzem o estágio de equilíbrio mais simples: a partir deles temos a saída de uma corrente de líquido e uma de vapor. E, por isso, eles são tão importantes. Quase tudo que aprendermos sobre eles pode ser aplicado para outros equipamentos!
E o que vai ser isso que vamos aprender sobre eles para aplicar também em outros equipamentos?
A famosa Equação de Flash!
Obtendo a Equação de Flash
Para obtermos a Equação de Flash, vamos precisar combinar algumas notações.
A corrente que entra no flash vai ser chamada de carga e será representada pela letra . Como essa corrente pode ser líquida, vapor ou os dois, vamos dizer que a composição dessa corrente é representada por .
A corrente de líquido que sai no fundo será chamada de , com composição . Enquanto que a corrente de vapor que sai no topo será chamada de , com composição .
Assim, podemos escrever o balanço de massa global do nosso flash:
O balanço por componente fica assim:
Se a gente dividir tudo pela nossa carga , obtemos que:
E a partir daí vamos definir uma coisa importante que vamos usar em TUDO daqui para frente. Vamos chamar a fração vaporizada, ou seja, de . Então, podemos substituir isso na nossa fórmula de balanço de massa por componente.
E será que conseguimos substituir nosso por alguma coisa?
Sabemos que . Então, dividindo tudo por também:
Só que , então já sabemos escrever em função de .
Logo, podemos substituir isso no nosso balanço de massa por componente.
Aí podemos colocar o em evidência:
Ou o :
Vamos guardar essas duas equações um pouquinho e pensar no somatório das frações.
A gente sabe que no equilíbrio o somatório do para todos os componentes é igual a . Assim como o do . Então se subtrairmos os dois somatórios (cada um é igual a 1), obtemos zero como resposta, né?
Reorganizando:
Bora colocar o em evidência?
E nós já vimos que , então vamos substituir.
Agora vamos pegar aquela equação que a gente tinha obtido antes, pelo balanço de massa por componente. Podemos reescrever ela:
E substituir o que apareceu ali no nosso somatório:
E aí conseguimos de novo substituir por , lembrando .
E essa é a nossa Equação de Flash, que só serve para duas fases!!!
Lembrete: é a fração vaporizada, que só pode variar de 0 até 1.
Dica: Se a partir de , você quiser trabalhar com ou , pode usar essas equações aqui:
Simplificações da Equação de Flash
Podemos fazer algumas simplificações da Equação de Flash quando estamos em “casos limite”.
Quando temos , o sistema está totalmente líquido, com exceção de uma bolha de vapor. E caso, estamos querendo dizer que o sistema está totalmente vaporizado, com exceção de uma gota de líquido.
Vamos avaliar as simplificações quando nosso . Nesse caso, nossa equação do Flash pode ser reescrita como:
Podemos abrir essa equação em dois termos:
Como o somatório de todas as composições globais tem que ser um, temos que:
Essa então vai ser a nossa Equação de Flash para quando só temos uma bolha de vapor, ou seja, equação de bolha.
A próxima simplificação ocorrerá para o , ou seja, temos apenas uma gotinha de líquido. Portanto, a equação que vamos obter nessa simplificação é a equação do ponto de orvalho. Saca só:
Simplificando:
Abrindo essa equação:
Podemos cortar ali o no primeiro termo, já que ele aparece no denominador e numerador.
Como o somatório do deve ser igual a .
E essa é nossa equação para o ponto de orvalho!!!
Resumão
Vou resumir as três equações e quando você vai precisar usar, ok?
Falou que a mistura é parcialmente vaporizada? Flash completão!!
Falou de ponto de bolha, primeira bolha de vapor e etc? Ou então falou que o . Usa essa equação aqui:
Por fim, se falar de ponto de orvalho, última gota de líquido ou . Só aplicar essa equação:
Ficou bem mais simples com nosso resumão né? Se sua prova tiver formulário, coloca essas equações lá e o significado do , pois COM CERTEZA vai cair na sua prova!
Simplificações da Equação de Flash
Resumão
Exercícios Resolvidos
Exercício Resolvido #1
Concurso CESPE, Órgão CPRM, 2013. Analista em Geociências - Química
Considerando que os processos de destilação permitem realizar a separação de dois ou mais componentes em função de diferenças nas volatilidades relativas desses componentes, julgue o item subsequente.
Na destilação flash, o aquecimento súbito de uma mistura líquida permite separar os componentes dessa mistura com diferentes pontos de ebulição.
( ) Certo
( ) Errado
Passo 1
Vamos lá!
Para resolver essa questão teórica precisamos relembrar o que vimos sobre flash, beleza?
Vimos que flash, ou colunas de flash, são equipamentos que podem agir por dispositivos térmicos ou mecânicos. Com a diferença de temperatura ou de pressão observada, haverá a separação da corrente inicial (que pode ser líquida, vapor ou mistura deles) em duas novas correntes. Essas duas novas correntes serão uma líquida e outra vapor!!
Olha a figurinha abaixo com um flash térmico para te ajudar a relembrar.
Passo 2
Além da parte teórica, vimos as equações relacionadas ao flash. E o coração da nossa equação de flash é o .
O é importante para lembrarmos que não existe uma separação completa, tipo assim, o composto não vai todo para fase vapor ou todo para fase líquida. Tem sempre uma constante (para cada composto, em cada temperatura e pressão), que vai relacionar a concentração nas duas fases.
Então, vamos separar a corrente de entrada em duas correntes, uma líquida e uma vapor. Mas as duas correntes vão apresentar uma mistura de componentes, e não os componentes puros.
Portanto, a separação completa de compostos com diferentes temperaturas de ebulição não ocorre, pois sempre fica um pouquinho na outra fase. Assim, a afirmativa está errada ☹
Resposta
Errado
Exercício Resolvido #2
Questão 1, Lista 1, Operações Unitárias 2 - UFRJ
Determine a composição do vapor que se encontra em equilíbrio com a mistura líquida (que entra no flash) de composição: 20 moles % de benzeno, 40 moles % de tolueno e 40 moles % de p-xileno a e .
Passo 1
Primeira coisinha que precisamos fazer em questões de flash é tentar entender a composição e informações de todas as correntes que temos.
Nesse caso, a mistura que está entrando no flash, e , possui a seguinte composição global:
Onde será nossa notação para o benzeno, para o tolueno e para o p-xileno.
Nosso objetivo final é o cálculo do de cada um dos compostos, para isso precisaremos utilizar a equação de flash e fazer o cálculo do . Mas vamos aos pouquinhos para não ficar confuso, ok?
Passo 2
Estamos falando de flash, então vamos precisar falar sobre e sobre as nossas velhas equações para achar.
Nós iremos considerar a seguinte equação para :
Obs: Seu professor pode utilizar uma equação diferente, mas aqui vamos utilizar como exemplo a Equação de Antoine nesse formato. Esse formato é o adotado pelo livro Smith Van Ness. A pressão está em e a temperatura está em .
Assim, vamos pegar as constantes para esses componentes na nossa tabela!
Passo 3
Calculando então as para cada componente:
Então, obtemos que:
Como conhecemos o e sabemos a pressão de operação (), podemos só substituir na fórmula e encontrar o para cada um deles!!!
Passo 4
Agora que conhecemos os podemos substituir todos os dados que temos na equação de flash e com isso encontrar a nossa única incógnita que será o !
Portanto:
Passo 5
Agora que já encontramos nosso famoso , podemos usá-lo para encontrar a composição de vapor da corrente, ou seja, nossos , através da seguinte equação:
Bora calcular essa galera! 😊
Como o nosso é super alto, a maior parte da corrente está na fase vapor. Então é normal que a composição do vapor seja bem próxima à composição global da corrente de entrada.
Podemos também calcular a composição do líquido, saca só:
Resposta
Exercício Resolvido #3
Concurso Eletrobras, 2002. Cargo: Engenheiro, Área: Química
Uma mistura binária é alimentada a um tambor de "flash" ("destilação integral") que opera no estado estacionário. A constante de equilíbrio de fases do composto A ( , na qual e representam, respectivamente, as frações molares do composto A nas fases vapor e líquida) é igual a 5 e a do composto B é igual a 0,5. O "flash" separa a mistura em duas correntes, uma líquida e outra vapor de igual vazão molar. A fração molar do composto A na corrente de alimentação ao "flash" é igual a:
a) 0,1
b) 0,2
c) 0,25
d) 0,333...
e) 0,666...
Passo 1
Vamos começar entendendo o que a questão pede para a gente calcular.
Nós precisamos determinar a fração molar de A na alimentação, em outras palavras, precisamos encontrar o .
Para isso, podemos tentar trabalhar com a nossa equação de Flash:
Sendo que os foram dados, mas ainda precisamos determinar o . Então é por aí que vamos começar!
Passo 2
Bem, se você leu essa questão e não encontrou o valor da porcentagem que foi vaporizada, relaxa! A questão não informa isso, mas deixa de uma forma beeem sutil um caminho para a gente calcular, beleza?
A questão diz que “o ‘flash’ separa a mistura em duas correntes, uma líquida e outra vapor de igual vazão molar”. Isso significa que o e , que saem do flash tem vazões molares iguais. Então, vamos dar uma olhada no equipamento de flash.
Se a gente fizer o balanço de massa, vamos ter:
Onde é a notação que usamos para carga. E como , obtemos que:
Para o , a gente sabe que ele é igual a:
Ou seja, nossa fração vaporizada! Nesse caso particular então:
Passo 3
Agora, vamos substituir os dados na nossa equação e ver o que falta!
Lembrando que e .
Porém, temos duas incógnitas ( e ). Então, como resolver isso!?
Bem, se só temos dois compostos na alimentação podemos dizer que a composição deles soma ! Portanto:
Logo:
Substituindo:
E resolvendo essa equação, obtemos que:
Assim, a resposta certa é a letra d!!!!
Resposta
Letra d)
Exercício Resolvido #4
INEP 2005, ENADE, Química
Uma mistura binária contendo 50% molar de A e 50% molar de B é separada por destilação em flash a e . Considere o diagrama de equilíbrio de fases desta mistura a , mostrado abaixo.
Quais são as frações molares de A na corrente líquida e na corrente vapor ( e , respectivamente) e qual a razão entre a taxa da corrente de vapor e a taxa da corrente de alimentação()?
Passo 1
Pra resolver essa questão, a primeira coisa que precisamos fazer é localizar qual fase está em cada parte do gráfico!
Nós sabemos que nas temperaturas maiores temos vapor e nas menores temos líquido. E dentro do nosso “envelope” temos uma mistura de líquido e vapor em equilíbrio!
Passo 2
Para resolver a primeira parte da pergunta e determinar as composições da fase líquida e vapor, precisamos achar o ponto no gráfico da nossa carga (temos temperatura e composição).
Marquei esse ponto com uma estrela, tá?
Passo 3
A próxima coisa que precisamos fazer é determinar a composição do líquido e do vapor. Para isso vamos olhar na isoterma que traçamos em , ou seja, na linha com temperatura constante que fizemos, em que composição ela toca a curva do líquido e em que composição ela toca a curva do vapor, beleza?
Lendo esse gráfico vemos que no líquido e para o vapor
Portanto, a única resposta seria letra d), mas vamos continuar para calcular o , também conhecido como , para confirmar nossa questão!
Passo 4
Para achar nosso , vamos precisar trabalhar com balanço de massa!
Sabemos que:
Pois tudo que entra no flash (carga ) tem que sair (e).
Mas ainda precisamos de mais uma equação. Então podemos fazer um balanço por componente e utilizar as composições que nós temos:
Como nós queremos determinar , vamos dividir tudo por , então:
E lá da teoria nós vimos que:
Então:
Agora, é só substituirmos nossas composições e acharmos o .
Portanto,
Uhul!!! Bateu com a resposta que tínhamos da letra d)!!!!!
Resposta
Letra d)
Exercício Resolvido #5
Questão 5, Lista 1, Operações Unitárias 2 – UFRJ
Dois tanques de flash são colocados conforme figura a seguir. A pressão de ambos é . A carga que entra no primeiro tanque é uma solução aquosa de metanol a molar. A vazão da carga é de . O segundo tanque opera com e a composição do líquido é de molar de metanol. Determine:
a) A fração vaporizada no primeiro tanque
b) , , , e .
Passo 1
Primeira coisinha que precisamos fazer em questões de flash é tentar entender a composição e informações de todas as correntes que temos.
Vamos preencher na própria figura da questão!
E precisamos determinar:
a) A fração vaporizada no primeiro tanque, ou seja,
b) , , , e , ou seja, a composição do vapor nos dois flashes, a composição do líquido no primeiro flash e a temperatura de operação desses caras.
Como conhecemos a saída do tanque 2 e o dele, vamos começar resolvendo tudo do tanque 2 e depois vamos para o tanque 1.
Passo 2
Nesse caso, nós vamos começar trabalhando com a corrente líquida de saída do segundo tanque. Vamos utilizar a corrente de saída, pois a partir dela vamos achar a temperatura do nosso segundo tanque!
Como a corrente de saída é líquida, podemos usar a simplificação para os casos onde . Então:
E nós sabemos como calcular em função das pressões parciais:
Então, substituindo na fórmula do flash simplificado:
E podemos obter através da Equação de Antoine:
Substituindo isso tudo na nossa equação de Flash simplificada para líquidos, obtemos que:
As constantes e da água e do metanolmsão tabeladas. O valor dessas constantes define a unidade da temperatura, a unidade da pressão e também se na equação de Antoine usamos ou . Então muita atenção para usar a equação adequada às suas constantes. Para a equação com , pressão em e temperatura em , temos os seguintes valores tabelados para as constantes:
E jogando elas na nossa fórmula e a composição dessa corrente de líquido, conseguimos achar a temperatura do tanque de flash 2 ().
Passo 3
Agora que já temos a temperatura, podemos calcular o para cada um dos nossos componentes.
E qual o nosso interesse no ? Ele tem mais uma forma de ser calculado, lembra?
Então através dele a gente consegue achar a especificação do vapor que tá saindo no topo da nossa coluna 2!
Até o momento, estamos com as seguintes informações então:
Passo 4
Então, a próxima coisa que precisamos calcular é a entrada do tanque 2 e para isso vamos utilizar a seguinte equação:
Sabendo que nosso é a mesma coisa que e foi dado na questão como , vamos substituit tudo aí na questão:
Portanto:
Logo:
Pois:
Então, temos agora todas essas correntes especificadas:
Passo 5
Vamos começar a falar sobre o tanque 1!
A saída do fundo (líquido) do tanque 1 é a entrada do tanque 2, que já especificamos, certo?
Portanto:
Então, como temos a composição do líquido especificada, podemos fazer o mesmo procedimento do tanque 2 (Passo 2) para calcular a temperatura do tanque 1.
Passo 6
Analogamente ao tanque 2 (Passo 3), vamos calcular os , já que já temos a temperatura, para depois conseguirmos achar os .
Utilizando novamente a definição de , temos como achar a composição do vapor que está saindo do tanque 1.
Passo 7
Última coisa que precisamos calcular nessa questão enorme é o do tanque 1. E, para calculá-lo, vamos recorrer a nossa equação de , já que temos todos os dados que precisamos!
Achando o .
E assim fica nosso esquema com todos os cálculos feitos. E essa é a nossa resposta final!
Resposta
