Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Caso Colunas com soluções diluídas

Ver Todos os Exercícios

Teoria

Introdução

Falaaaaa aiii, tudo chuchu beleza? Nesse tópico vamos falar de colunas com soluções diluídas, mas antes, você sabe o que são soluções diluídas?

Soluções diluídas são aquelas em que a quantidade de soluto é muito pequena em relação à de solvente, sendo assim, a solução se encontra completamente diluída. Pensa naquele suco em pó aguado em que quando você toma faz uma cara tipo assim:

Esse suco em pó aguado é uma solução diluída. Então vamos ver como as colunas funcionam com elas!

Balanço de massa global

Temos para um balanço de massa genérico:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Para o caso do balanço de massa global da coluna, o que entra é:

V 1 ' y A 1 + L 2 ' x A 2

O que sai da coluna é:

V 2 ' y A 2 + L 1 ' x A 1

Sendo que normalmente não vai ocorrer geração de um produto, pois costumamos considerar que não irão ocorrer reações químicas. Nesse caso:

G e r a d o = 0

A variação também vai ser um termo nulo, pois a coluna opera em regime permanente, ou seja, não ocorre mudanças com o tempo. Logo,

V a r i a ç ã o = 0

Juntando tudo temos:

V 1 ' y A 1 + L 2 ' x A 2 - V 2 ' y A 2 + L 1 ' x A 1 + 0 = 0

V 1 ' y A 1 + L 2 ' x A 2 = V 2 ' y A 2 + L 1 ' x A 1

Simplificações para coluna com solução diluída

Se a solução é diluída, a variação de L ’ e G ' ao longo da coluna é pequena. No geral as frações molares de até 0,05 de contaminante na entrada da coluna podem ser consideradas como solução diluída, beleza?

Considerando que a diluição é diluída temos:

V 1 ' = V 2 ' = V '

L 2 ' = L 1 ' = L '

Então a equação do balanço global fica:

V ' y A 1 - y A 2 = L ' ( x A 1 - x A 2 )

Bora para os exercícios?

Fator de absorção

Definindo o fator de absorção como,

A = L V . m

Tendo que,

∆ y 1 = ∆ y o L V * m  

E,

∆ y o = y 1 - y 1 *

Onde y 1 *   é a composição do vapor em equilíbrio com x o ,

y 1 * = m * x o + b

Algumas relações para absorção

Podemos calcular o número de pratos a partir da relação:

y N + 1 - y 1 * y 1 - y 1 * = 1 - L V * m N + 1 1 - L V * m

Ou,

y N + 1 - y N + 1 * y 1 - y 1 * = L m * V N

Manipulando essa relação chegamos em,

N = ln ⁡ y N + 1 - y N + 1 * y 1 - y 1 *     ln ⁡ L m * V

Ou,

N = ln ⁡ y N + 1 - y N + 1 * y 1 - y 1 *     ln ⁡ y N + 1 - y 1 y N + 1 * - y 1 *

Algumas relações para esgotamento

Já para a parte do esgotamento podemos calcular o número de pratos a partir da relação:

x N - x N * x o - x N * = 1 - V * m L 1 - V * m L N + 1

Ou,

x N - x N * x o - x o * = m * V L N

Manipulando essa relação chegamos em,

N = ln ⁡ x N - x N * x o - x N *     ln ⁡ L m * V

Relaxa que essas fórmulas você não precisa decorar, beleza? Normalmente o professor vai ter dar na hora da prova.

Agora vamos exercitar! 😊

Simplificações para coluna com solução diluída

Fator de absorção

Algumas relações para absorção

Algumas relações para esgotamento

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Disserte um pouco sobre o que são colunas com soluções diluídas.

Passo 1

Fala aíii, tudo bem? Vamos ver agora sobre colunas com soluções diluídas!!

Passo 2

Colunas com soluções diluídas são colunas de destilação em que a quantidade de soluto é muito pequena em relação à de solvente, sendo assim, a solução se encontra completamente diluída.

Resposta

Colunas com soluções diluídas são colunas de destilação em que a quantidade de soluto é muito pequena em relação à de solvente, sendo assim, a solução se encontra completamente diluída.

Exercício Resolvido #2

Elaboração própria

Deduza o balanço de massa de um uma coluna com solução diluída.

Passo 1

Falaaaa aí! Bora deduzir esse balanço de massa lembrando da regrinha genérica que diz:

E n t r a - S a i + G e r a d o = V a r i a ç ã o

Agora só precisamos adicionar nossas considerações.

Passo 2

Vamos analisar cada termo da equação de cima, começando pelo que entra na coluna:

E n t r a = G 1 ' y A 1 + L 2 ' x A 2

E o que sai,

S a i = G 2 ' y A 2 + L 1 ' x A 1

E vamos considerar que tanto o gerado como a variação como um termo nulo, ou seja,

G e r a d o = V a r i a ç ã o = 0

O gerado ser zero significa que estamos desprezando as reações químicas e a variação ser zero indica que estamos operando em regime permanente.

Passo 3

Agora podemos juntar tudo e obter:

G 1 ' y A 1 + L 2 ' x A 2 - G 2 ' y A 2 + L 1 ' x A 1 + 0 = 0

Simplificando isso temos,

G 1 ' y A 1 + L 2 ' x A 2 = G 2 ' y A 2 + L 1 ' x A 1

Passo 4

Se a solução é diluída, a variação de L ’ e G ' ao longo da coluna é pequena. Logo,

G 1 ' = G 2 ' = G '

L 2 ' = L 1 ' = L '

Então a equação do balanço global fica:

G ' y A 1 - y A 2 = L ' ( x A 1 - x A 2 )

Resposta

G ' y A 1 - y A 2 = L ' ( x A 1 - x A 2 )

Exercício Resolvido #3

Elaboração própria

Calcule o fator de absorção sabendo que em uma coluna de destilação tem como entrada ar a 30   m 3   por m 3 rejeito aquoso.

Dado: y = 2 x

Passo 1

Oi oi oiee, tudo bem? Nessa questão nós queremos calcular o fator de absorção, A , e para isso vamos usar a seguinte expressão:

A = L V . m

Sendo que o enunciado nos forneceu,

V L = 30 m 3 ( a r ) 1 m 3 ( r e j e i t o   a q u o s o )

E,

y = 2 x

Passo 2

Agora você deve estar pensando, mas e como eu vou calcular o fator de absorção sem o m ? Repara que ele nos deu,

y = 2 x

Sendo que,

y = m * x

Logo,

m = 2

Passo 3

Agora podemos substituir os valores na expressão do fator de absorção:

A = L V . m

Mas repara que nós já sabemos,

V L = 30 m 3 ( a r ) 1 m 3 ( r e j e i t o   a q u o s o )

Então,

A = 1 30 * 2 = 0,067

A = 0,067

Resposta

A = 0,067

Exercício Resolvido #4

Adaptado - Caderno de Operações Unitárias 2, Profa. Silvia, UFRJ

É necessário remover H 2 S e C O 2 na corrente gasosa de vazão molar 1000   k m o l / h de H 2 O   a 0 ° C e 15,5   a t m . O líquido de entrada contém 2,4 × 10 - 5 fração molar de H 2 S e 3,8 × 10 - 5 fração molar de C O 2 . Deseja-se 99 % de recuperação de H 2 S na fase gasosa de saída. O gás é N 2 puro a 0 ° C e 15,5   a t m . O fluxo de N 2 é 3,44   k m o l / h . Uma coluna de pratos será usada para o esgotamento. Assume-se que o fluxo de H 2 O e N 2 sejam constantes.

Determine a composição de H 2 S no produto líquido e gasoso.

Passo 1

Fala aíii, tudo bem? Antes de tudo vamos passar um raio X nesse enunciado. Vamos considera o índice “1” vai ser referente ao H 2 S e o índice “2” referente ao C O 2 . Com isso temos,

x o 1 = 2,4 × 10 - 5

x o 2 = 3,8 × 10 - 5

Lembrando que precisamos recuperar 99 % de H 2 S na fase gasosa de saída. Além disso, temos:

V = 3,44   k m o l / h   ( N 2 )

L = 1000   k m o l / h   ( H 2 O )

E com essas informações vamos encontrar a composição de H 2 S no produto líquido e gasoso.

Passo 2

Antes de tudo vamos calcular a vazão molar de H 2 S na corrente de entrada. Começando pela fase líquida,

m 1 ˙ = L * x o 1

Substituindo os valores,

m 1 ˙ = 1000   k m o l / h   * 2,4 × 10 - 5

m 1 ˙ = 0,024 k m o l / h   ( H 2 S )

Passo 3

Calculando agora a vazão molar na fase gasosa, lembrando que queríamos recuperar 99 % de H 2 S .

m 1 ˙ ( r e c u p e r a d o ) = 0,99 * m 1 ˙

m 1 ˙ ( r e c u p e r a d o ) = 0,99 * 0,024 k m o l / h

m 1 ˙ r e c u p e r a d o = 0,02376   k m o l / h   ( H 2 S )

E o que não foi recuperado vai para fase líquida,

m 1 ˙ ( p e r d i d o ) = 0 , 01 * 0,024 k m o l / h

m 1 ˙ p e r d i d o = 2,4 × 10 - 4 k m o l / h   ( H 2 S )

Passo 4

Já com a vazão do H 2 S recuperado e perdido em mãos podemos, finalmente, calcular a composição de H 2 S no produto líquido e gasoso.

No produto líquido temos,

x N 1 = m 1 ˙ p e r d i d o L

Substituindo os valores,

x N 1 = 2,4 × 10 - 4 k m o l / h   1000   k m o l / h

x N 1 = 2,4 × 10 - 7  

Passo 5

Por fim, para o produto gasoso temos,

y 1 1 = m 1 ˙ r e c u p e r a d o V

Substituindo os valores,

y 1 1 = 0,02376   k m o l / h   3,44   k m o l / h   ( N 2 )

y 1 1 = 6,906 × 10 - 3  

Resposta

x N 1 = 2,4 × 10 - 7  

y 1 1 = 6,906 × 10 - 3  

Exercício Resolvido #5

Adaptado - Caderno de Operações Unitárias 2, Profa. Silvia, UFRJ

É necessário remover H 2 S e C O 2 na corrente gasosa de vazão molar 1000   k m o l / h de H 2 O   a 0 ° C e 15,5   a t m . O líquido de entrada contém 2,4 × 10 - 5 fração molar de H 2 S e 3,8 × 10 - 5 fração molar de C O 2 . Deseja-se 99 % de recuperação de H 2 S na fase gasosa de saída. O gás é N 2 puro a 0 ° C e 15,5   a t m . O fluxo de N 2 é 3,44   k m o l / h . Uma coluna de pratos será usada para o esgotamento. Assume-se que o fluxo de H 2 O e N 2 sejam constantes.

Determine o número de estágios de equilíbrio.

Passo 1

Fala aíii, tudo bem? Nessa questão nós queremos calcular o número de estágios de uma coluna de esgotamento. Ou seja, vamos utilizar a seguinte expressão,

N = ln ⁡ x N - x N * x o - x N *     ln ⁡ L m * V

O enunciado nos forneceu,

x o 1 = 2,4 × 10 - 5

x o 2 = 3,8 × 10 - 5

V = 3,44   k m o l / h   ( N 2 )

L = 1000   k m o l / h   ( H 2 O )

Considerando que o índice “1” vai ser referente ao H 2 S e o índice “2” referente ao C O 2 . E nós vamos encontrar o número de estágio com base no   H 2 S .

Passo 2

Para calcular o número de estágios precisamos primeiro calcular m 1 ˙ e x N . Temos que,

m 1 ˙ = L * x o 1 = 1000   k m o l / h   * 2,4 × 10 - 5 = 0,024 k m o l / h   ( H 2 S )

Mas para encontrar   x N precisamos encontrar a vazão do recuperado e do perdido. Lembrando que queremos recuperar 99 % de H 2 S . O que foi para fase líquida é o recuperado,

m 1 ˙ ( r e c u p e r a d o ) = 0,99 * 0,024 k m o l / h = 0,02376   k m o l / h   ( H 2 S )

E com isso temos,

x N 1 = m 1 ˙ p e r d i d o L = 2,4 × 10 - 4 k m o l / h   1000   k m o l / h = 2,4 × 10 - 7  

Passo 3

Já para a fase gasosa temos,

m 1 ˙ ( p e r d i d o ) = 0,01 * 0,024 k m o l / h = 2,4 × 10 - 4 k m o l / h   ( H 2 S )

Logo,

y N 1 = m 1 ˙ r e c u p e r a d o V = 0,02376   k m o l / h   3,44   k m o l / h   ( N 2 ) = 6,906 × 10 - 3  

Passo 4

Já com a vazão do H 2 S recuperado e perdido em mãos podemos, finalmente, calcular a composição de H 2 S no produto líquido e gasoso.

No produto líquido temos,

x N 1 = m 1 ˙ p e r d i d o L

Substituindo os valores,

x N 1 = 2,4 × 10 - 4 k m o l / h   1000   k m o l / h

x N 1 = 2,4 × 10 - 7  

Beleza, já temos o x N 1 , mas agora precisamos calcular x N 1 * e para isso vamos encontrar y 1 1 .

Passo 5

Para o produto gasoso temos,

y 1 1 = m 1 ˙ r e c u p e r a d o V

Substituindo os valores,

y 1 1 = 0,02376   k m o l / h   3,44   k m o l / h   ( N 2 )

y 1 1 = 6,906 × 10 - 3  

Logo,

x N 1 * = y 1 1 m 1 ˙ = 6,906 × 10 - 3 0,024 = 0 , 28775

Passo 6

Substituindo agora os valores dados e os calculados na equação do número de estágios temos,

N = ln ⁡ x N 1 - x N 1 * x o 1 - x N 1 *     ln ⁡ L m 1 ˙ * V

N = ln ⁡ 2,4 × 10 - 7 - 0,28775 2,4 × 10 - 5 - 0,28775     ln ⁡ 1000   0,024 * 3,44   = 3

Resposta

N = 3

Exercício Resolvido #6

Exemplo 4, Chapter 20 McCabe et al 7th edition 2005

Uma mistura líquida com   2,0   % molar de etanol e 98 % molar água é submetida a uma operação de stripping com vapor de água pura (fluido de arraste) numa col una de estágios com fluxos contra correntes. O produto de fundo da coluna deve conter 0,01   % molar de etanol . A alimentação da m istura líquida encontra -se na temperatura do ponto de bolha (líquido saturado) e a corrente de vapor à saída da coluna é 0,2   moles por cada mol de alimentação . Para soluções diluí das de etanol - água pode em pregar a seguinte relação de equilíbrio y e = 9,0 x e . Quantos estágios ideais são necessários para a separação ?

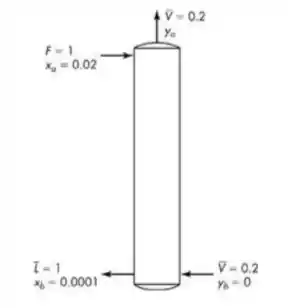
Passo 1

Faaala aíii, tudo show de bola? A coluna dessa questão é similar a uma coluna de absorção, onde a alimentação na forma de vapor entra à base da coluna a solução líquida no topo da coluna.

Onde temos,

m = 9,0

y b = 0

x a = 0,02

x b = 0,0001

E a partir dessas informações vamos calcular o número de estágios com,

N = ln ⁡ y N + 1 - y N + 1 * y 1 - y 1 *     ln ⁡ L m * V

Ou,

N = ln ⁡ y N + 1 - y N + 1 * y 1 - y 1 *     ln ⁡ y N + 1 - y 1 y N + 1 * - y 1 *

Passo 2

Como,

y e = 9,0 x e

Logo,

y a * = m x a = 9,0 × 0,02 = 0,18

y b * = 9,0 × 0,0001 = 0,0009

Para fazer os cálculos vamos supor que:

F = 1,0   m o l   ( l í q u i d o   s a t u r a d o )

E,

F = L = 1,0

V = 0,2

Passo 3

Calculando o fator de absorção,

A = L m V = 1 0,2 × 9 = 0,555

Fazendo agora o balanço material da coluna para calcular y a temos para misturas diluídas,

V y a - y b = L ( x a - x b )

Substituindo os valores,

0,2 y a - 0 = 1 ( 0,02 - 0,0001 )

y a = 0,0995

Passo 4

Calculando agora o número de estágios necessários temos:

N = ln ⁡ y N + 1 - y N + 1 * y 1 - y 1 *     ln ⁡ y N + 1 - y 1 y N + 1 * - y 1 *

Substituindo os valores temos,

N = ln ⁡ 0,0995 - 0,18 0 - 0,0009     ln ⁡ 0,0009 - 0,18 0 - 0,0995 = ln ⁡ 89,4 ln ⁡ 1,8 = 7,6

Ou seja, serão necessários 8 estágios.

Repara que você poderia ter usado,

N = ln ⁡ y N + 1 - y N + 1 * y 1 - y 1 *     ln ⁡ L m * V

Que o resultado final daria no mesmo, beleza? 😉

Resposta

N = 8

Exercício Resolvido #7

Caderno de Operações Unitárias 2, Profa. Silvia, UFRJ

Uma coluna com seis estágios de equilíbrio é empregada para esgotar uma corrente líquida com ar a 80 ° F e P = 1 a t m . Calcule a concentração de amônia na corrente líquida aquosa de saída se a concentração do líquido na entrada é 0,1 % molar de amônia em H 2 O . O ar de entrada é livre de amônia e 30   S C F de são alimentados na coluna por libra de rejeito aquoso.

Dados: y = 1,414 x , S C F   = S t a n d a r t   C u b i c   F e e t

Passo 1

Faaaala aíi! Vamos começar aqui analisando o que a questão nos forneceu, beleza? Aqui estamos lidando com uma coluna de esgotamento, logo, vamos usar a expressão:

x N - x N * x o - x N * = 1 - V * m L 1 - V * m L N + 1

Já tendo pelo enunciado,

N = 6

y 7 = 0

x o = 0,001

y = 1,414 x

V L = 30   f t 3 a r 1   l b m H 2 O

E queremos encontrar a concentração de amônia na corrente líquida aquosa de saída, ou seja, x 6 .

Passo 2

Antes de mais nada precisamos ajustar as unidades da nossa relação V / L ,

V L = 30   f t 3 a r 1   l b m H 2 O × 18   l b m H 2 O 1   l b m o l H 2 O × 1 l b m o l H 2 O 393,95034   f t 3 a r

V L = 1,37 l b m o l ( a r ) l b m o l ( H 2 O )

Agora sim as unidades batem e podemos analisar a correlação para colunas de esgotamento.

Passo 3

Já vimos que vamos utilizar,

x N - x N * x o - x N * = 1 - V * m L 1 - V * m L N + 1

Se adequando a nossa questão temos,

x 6 - x 6 * x o - x 6 * = 1 - V * m L 1 - V * m L 7

Daqui ainda não temos x 6 * ,

x 6 * = y 7 m = 0 m = 0

Mas precisamos do m   também. O enunciado nos deu,

y = 1,414 x

Sendo que,

y = m * x

Logo,

m = 1,414

Passo 4

Agora, finalmente, substituindo os valores na equação temos,

x 6 - 0 0,001 - 0 = 1 - 1,44 * 1,37 1 - 1,44 * 1,37 7

Lembrando que calculamos o V / L no passo 2, o x 6 * no passo 3 e o resto é dado do enunciado. Fazendo as contas,

x 6 0,001 = 9,2447 × 10 - 3  

Logo,

x 6 = 9,2447 × 10 - 6  

Resposta

x 6 = 9,2447 × 10 - 6  

Exercício Resolvido #8

Adaptado - Exemplo 17.2 – Operaciones Unitárias em Engenharia Química, Marren L. McCabe, Julian C. Smith, Peter Harriot

A amônia é dessorvida de uma solução aquosa diluída pelo contato em contracorrente com o ar em uma coluna contendo sete placas perfuradas. A razão de equilíbrio é y e   =   0,8 x e , e quando o fluxo molar de ar é 1 , 5 vezes o da solução, 90 %   da amônia é removida. Quantos estágios ideais a coluna deve ter e qual é a eficiência dos estágios?

Passo 1

Fala aii, tudo bem? Nessa questão nós temos uma solução aquosa contendo 7 estágios. Onde a razão de equilíbrio é:

y   =   0,8 x

E,

V L = 1,5

Onde 90 % da amônia é removida. A partir disso vamos calcular o número de estágios ideais a coluna deve ter e qual é a eficiência dos estágios. Ou seja, vamos usar a equação,

N = ln ⁡ x N - x N * x o - x N *     ln ⁡ L m * V

Passo 2

Antes de tudo vamos calcular o fator de absorção,

A = L m V = 0,8 1,5 = 0,53

Todas as concentrações podem ser expressas como uma função de x a , que é a fração molar de NH. Na entrada da solução temos,

x b = 0,1 x a

x b * = 0

Pois,

y b = 0

Passo 3

A partir do balanço da amônia temos,

V ∆ y = V y a = L

∆ x = L ( 0,9 x a )

Logo,

y a = L V 0,9 x = 0,9 1,5 x a = 0,6 x a

E,

x a * = y a m = 0,6 x a 0,8 = 0,75 x a

Passo 4

Agora podemos finalmente calcular o número de estágios com,

N = ln ⁡ x N - x N * x o - x N *     ln ⁡ L m * V

Substituindo os valores temos,

N = ln ⁡ 0,8 x a - 0,75 x a x a - 0,75 x a     ln ⁡ 0,53 = 5,0

Logo, a separação corresponde a 5,0 estágios ideais, de forma que a eficiência dos estágios é:

5,0 7 × 100 %   =   72 %  

Resposta

5   e s t á g i o s   c o m   e f i c i ê n c i a   d e   72 %