Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Extração e Tipos de Sistemas

Ver Todos os Exercícios

Teoria

Introdução

Faaaaaaala aiii, tudo belezura? Vamos iniciar agora o nosso papo sobre colunas de extração líquido-líquido e os seus tipos de sistema.

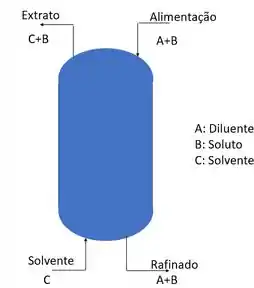
Só para entender melhor para onde estamos indo, a extração-líquido-líquido ocorre quando uma mistura líquida a ser separada (soluto+diluente) é colocada em contato com outro líquido (solvente).

Uma coisa importante de se ter em mente é que na extração não envolve vaporização, então, pode ser realizada a temperaturas mais baixas, o que torna o processo atraente.

Separação de fases

No sistema de extração líquido-líquido ocorre a separação de duas fases. Para isso, é necessário que o diluente e o solvente sejam parcialmente miscíveis ou completamente imiscíveis. Além disso, o solvente deve ter grande afinidade com o soluto.

Mas afinal quais são essas duas fases??

A primeira fase vamos chamar de rafinado. Esta fase é rica no diluente e contém pequenas quantidades de soluto não extraído. Já a segunda fase vamos chamar de extrato, que é a fase rica no solvente e contém soluto extraído.

Tipos de sistemas

O processo de extração líquido-líquido apresenta-se como uma alternativa das mais viáveis para sistemas diluídos, quando se utiliza solventes apropriados e de baixa toxicidade.

Além disso, pode se ter também sistemas ternários com um par de solventes imiscíveis ou dois pares de solventes imiscíveis. Vamos analisar melhor esses sistemas quando falarmos sobre os diagramas de fases deles.

Relação de equilíbrio

Um cara que também vai ser importante pra gente é o coeficiente de distribuição K d . E ele é nada mais, nada menos do que a razão entre a fração molar do solvente (extrato) e a fração molar do soluto (rafinado). Ou seja,

K d = y x

Mas agora que tal partir para os exercícios? 😉

Separação de fases

Tipos de sistemas

Relação de equilíbrio

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Explique em poucas palavras a extração líquido-líquido.

Passo 1

Falaaa aíii, vamos iniciar nossos exercícios relembrando o que é extração líquido-líquido, beleza?

Passo 2

Basicamente a extração-líquido-líquido ocorre quando uma mistura líquida a ser separada (soluto+diluente) é colocada em contato com outro líquido (solvente).

Resposta

Basicamente a extração-líquido-líquido ocorre quando uma mistura líquida a ser separada (soluto+diluente) é colocada em contato com outro líquido (solvente).

Exercício Resolvido #2

Elaboração própria

Qual é a vantagem que podemos apontar para a extração líquido-líquido frente as outras?

Passo 1

Oi oi oii, aqui nós precisamos enxergar o que a extração líquido-líquido tem de mais vantajoso em relação as outras, beleza?

Passo 2

Como o próprio nome já diz, vai ser uma extração com apenas uma fase, líquida. Logo, na extração não envolve vaporização, então, pode ser realizada a temperaturas mais baixas, o que torna o processo mais atraente que as outras 😉

Resposta

A extração líquido-líquido não envolve vaporização, então, pode ser realizada a temperaturas mais baixas, o que torna o processo atraente.

Exercício Resolvido #3

Elaboração própria

Disserte sobre as duas fases que são separadas na extração líquido-líquido.

Passo 1

Heyyy, temos que no sistema de extração líquido-líquido ocorre a separação de duas fases. Para isso, é necessário que o diluente e o solvente sejam parcialmente miscíveis ou completamente imiscíveis.

Além disso, o solvente deve ter grande afinidade com o soluto, beleza?

Passo 2

A primeira fase vamos chamar de rafinado. Esta fase é rica no diluente e contém pequenas quantidades de soluto não extraído.

Já a segunda fase vamos chamar de extrato, que é a fase rica no solvente e contém soluto extraído.

Resposta

A primeira fase é o rafinado que é a fase rica no diluente e contém pequenas quantidades de soluto não extraído. Já a segunda fase vamos chamar de extrato, que é a fase rica no solvente e contém soluto extraído.

Exercício Resolvido #4

Elaboração própria

Quais são os principais tipos de sistema de uma extração líquido-líquido?

Passo 1

Fala aíii, tudo bem? Nós vimos que o processo de extração líquido-líquido apresenta-se como uma alternativa das mais viáveis para sistemas diluídos, quando se utiliza solventes apropriados e de baixa toxicidade.

Passo 2

Além disso, pode se ter também sistemas ternários com um par de solventes imiscíveis ou dois pares de solventes imiscíveis.

Logo, os principais tipos de sistema são: sistemas diluídos e sistemas ternários.

Resposta

Os principais tipos de sistema são: sistemas diluídos e sistemas ternários.

Exercício Resolvido #5

Adaptado - Questão 3, 7ª Lista de Exercícios – Operações unitárias III Extração Líquido-líquido, UERJ

(Wankat, 3 ed. – Cap. 13 – D10) Dioxano será extraído de duas soluções aquosas com benzeno em um sistema de 2 estágios em fluxo cruzado. A corrente de benzeno que alimenta cada estágio é pura ( y d i o x a n o   =   0 ) . A vazão de solvente em cada estágio é 50     k g / h . A vazão da alimentação do 1 º estágio é de 100     k g / h e é composta de 1,5 % em massa de dioxano.

Considere que benzeno e água são totalmente imiscíveis e que a vazão total de rafinado e extrato entrando e deixando cada estágio é constante. O equilíbrio para o dioxano que se distribui entre benzeno e água é dado por y d i o x a n o =   1,02   x d i o x a n o , sendo y d i o x a n o a fração mássica de dioxano no extrato (fase rica em benzeno) e x d i o x a n o , a fração mássica de dioxano no rafinado (fase aquosa).

Encontre a fração mássica de dioxano no rafinado que deixa o 2 º estágio.

Passo 1

Fala aíii, tudo bem? Antes de tudo respira fundo! Eu sei que o enunciado é grande, mas nós vamos fazer juntos

Mas vamos começar pegando todas as informações necessárias que o enunciado nos deu:

x a ,   F 1 = 0,015

x a ,   F 2 = 0,005

x a ,   S = 0

S = 50   k g / h

F 1 = 100   k g / h

F 2 = 70   k g / h

y d i o x a n o =   1,02   x d i o x a n o

Além disso, como o enunciado nos diz que os líquidos são completamente imiscíveis e as vazões são constantes temos,

S = E 1 = E 2

F 1 = R 1 = R 2

Lembrando que o que queremos encontrar é a fração mássica de dioxano no rafinado que deixa o 2 º estágio.

Passo 2

Show! Agora para efetivamente começarmos a questão podemos fazer um balanço de massa no primeiro estágio,

F 1 x a , F 1 + S x a , S = R 1 x a , R 2 + E 1 x a , E 2

Como R 1 e E 1 são correntes em equilíbrio,

x a , E 1 = 1,02 x a , R 1

Logo, substituindo os valores, temos,

100 * 0,015 + 50 * 0 = 100 * x a , R 1 + 50 * 1,02 * x a , R 1

x a , R 1 = 0,0099

E fazendo um balanço no segundo estágio:

R 1 x a , R 1 + S x a , S = R 2 x a , R 2 + E 1 x a , E 2

Como R 2 e E 2 são correntes em equilíbrio,

x a , E 2 = 1,02 x a , R 2

Logo, substituindo os valores, temos,

100 * 0,0099 + 50 * 0 = 100 * x a , R 2 + 50 * 1,02 * x a , R 2

x a , R 2 = 0,0066

Resposta

x a , R 2 = 0,0066

Exercício Resolvido #6

Adaptado - Questão 3, 7ª Lista de Exercícios – Operações unitárias III Extração Líquido-líquido, UERJ

(Wankat, 3 ed. – Cap. 13 – D10) Dioxano será extraído de duas soluções aquosas com benzeno em um sistema de 4 estágios em fluxo cruzado. A corrente de benzeno que alimenta cada estágio é pura ( y d i o x a n o   =   0 ) . A vazão de solvente em cada estágio é 50     k g / h . A vazão da alimentação do 1 º estágio é de 100     k g / h e é composta de 1,5 % em massa de dioxano.

A 2ª corrente de alime ntação possui uma vazão de 70     k g / h e é composta de 0,5 % em massa de dioxano. Esta 2ª corrente de alimentação é misturada ao rafinado que sai do segundo estágio, e esta mistura é alimentada ao 3º estágio.

Considere que benzeno e água são totalmente imiscíveis e que a vazão total de rafinado e extrato entrando e deixando cada estágio é constante. O equilíbrio para o dioxano que se distribui entre benzeno e água é dado por y d i o x a n o =   1,02   x d i o x a n o , sendo y d i o x a n o a fração mássica de dioxano no extrato (fase rica em benzeno) e x d i o x a n o , a fração mássica de dioxano no rafinado (fase aquosa).

Encontre a fração mássica de dioxano no rafinado que deixa o 3 º estágio.

Passo 1

Fala aíii, tudo bem? Antes de tudo respira fundo! Eu sei que o enunciado é grande, mas nós vamos fazer juntos

Além disso, também temos uma alimentação entre o estágio 2 e 3. Mas vamos começar pegando todas as informações necessárias que o enunciado nos deu:

x a ,   F 1 = 0,015

x a ,   F 2 = 0,005

x a ,   S = 0

S = 50   k g / h

F 1 = 100   k g / h

F 2 = 70   k g / h

y d i o x a n o =   1,02   x d i o x a n o

Além disso, como o enunciado nos diz que os líquidos são completamente imiscíveis e as vazões são constantes temos,

S = E 1 = E 2 = E 3 = E 4

F 1 = R 1 = R 2

F 1 + F 2 = R m i s t = R 3 = R 4

Lembrando que o que queremos encontrar é a fração mássica de dioxano no rafinado que deixa o 3 º estágio.

Passo 2

Show! Agora para efetivamente começarmos a questão podemos fazer um balanço de massa inicialmente no primeiro estágio,

F 1 x a , F 1 + S x a , S = R 2 x a , R 2 + E 2 x a , E 2

Como R 1 e E 1 são correntes em equilíbrio,

x a , E 1 = 1,02 x a , R 1

Logo, substituindo os valores, temos,

100 * 0,015 + 50 * 0 = 100 * x a , R 1 + 50 * 1,02 * x a , R 1

x a , R 1 = 0,0099

Passo 3

Fazendo o balanço de massa agora para o segundo estágio temos,

R 1 x a , R 1 + S x a , S = R 2 x a , R 2 + E 2 x a , E 2

Como R 2 e E 2 são correntes em equilíbrio,

x a , E 2 = 1,02 x a , R 2

Logo, substituindo os valores, temos,

100 * 0,0 099 + 50 * 0 = 100 * x a , R 2 + 50 * 1,02 * x a , R 2

x a , R 2 = 0,00 6 6

Mas nós queremos o rafinado do 3 º estágio. Então precisamos fazer um balanço no ponto de mistura.

Passo 4

Para o ponto de mistura temos,

R 1 x a , R 2 + F 2 x a , F 2 = R m i s t x a , R m i s t

Logo, substituindo os valores, temos,

100 * 0,00 66 + 7 0 * 0 , 005 = 1 7 0 * x a , R m i s t

x a , R m i s t = 0,00 59

Passo 5

Por fim, para o terceiro estágio temos o seguinte balanço,

R m i s t x a , R m i s t + S x a , S = R 3 x a , R 3 + E 3 x a , E 3

Como R 3 e E 3 são correntes em equilíbrio,

x a , E 3 = 1,02 x a , R 3

Logo, substituindo os valores, temos,

1 7 0 * 0,00 59 + 50 * 0 = 1 7 0 * x a , R 3 + 50 * 1,02 * x a , R 3

x a , R 3 = 0,00 46

Resposta

x a , R 3 = 0,0046

Exercício Resolvido #7

Adaptado - Questão 3, 7ª Lista de Exercícios – Operações unitárias III Extração Líquido-líquido, UERJ

(Wankat, 3 ed. – Cap. 13 – D10) Dioxano será extraído de duas soluções aquosas com benzeno em um sistema de 4 estágios em fluxo cruzado. A corrente de benzeno que alimenta cada estágio é pura ( y d i o x a n o   =   0 ) . A vazão de solvente em cada estágio é 50     k g / h . A vazão da alimentação do 1 º estágio é de 100     k g / h e é composta de 1,5 % em massa de dioxano.

A 2ª corrente de alime ntação possui uma vazão de 70     k g / h e é composta de 0,5 % em massa de dioxano. Esta 2ª corrente de alimentação é misturada ao rafinado que sai do segundo estágio, e esta mistura é alimentada ao 3º estágio.

Considere que benzeno e água são totalmente imiscíveis e que a vazão total de rafinado e extrato entrando e deixando cada estágio é constante. O equilíbrio para o dioxano que se distribui entre benzeno e água é dado por y d i o x a n o =   1,02   x d i o x a n o , sendo y d i o x a n o a fração mássica de dioxano no extrato (fase rica em benzeno) e x d i o x a n o , a fração mássica de dioxano no rafinado (fase aquosa).

Encontre a fração mássica de dioxano no rafinado e no extrato que deixa o 4 º estágio.

Passo 1

Fala aíii, tudo bem? Antes de tudo respira fundo! Eu sei que o enunciado é grande, mas nós vamos fazer juntos

Além disso, também temos uma alimentação entre o estágio 2 e 3. Mas vamos começar pegando todas as informações necessárias que o enunciado nos deu:

x a ,   F 1 = 0,015

x a ,   F 2 = 0,005

x a ,   S = 0

S = 50   k g / h

F 1 = 100   k g / h

F 2 = 70   k g / h

y d i o x a n o =   1,02   x d i o x a n o

Além disso, como o enunciado nos diz que os líquidos são completamente imiscíveis e as vazões são constantes temos,

S = E 1 = E 2 = E 3 = E 4

F 1 = R 1 = R 2

F 1 + F 2 = R m i s t = R 3 = R 4

Lembrando que o que queremos encontrar é a fração mássica de dioxano no rafinado e no extrato que deixa o 4 º estágio.

Passo 2

Para isso, vamos precisar fazer um balanço de massa em cada estágio. Começando pelo primeiro:

F 1 x a , F 1 + S x a , S = R 2 x a , R 2 + E 2 x a , E 2

Como R 1 e E 1 são correntes em equilíbrio,

x a , E 1 = 1,02 x a , R 1

Logo, substituindo os valores, temos,

100 * 0,015 + 50 * 0 = 100 * x a , R 1 + 50 * 1,02 * x a , R 1

x a , R 1 = 0,0099

E para o segundo,

R 1 x a , R 1 + S x a , S = R 2 x a , R 2 + E 2 x a , E 2

Como R 2 e E 2 são correntes em equilíbrio,

x a , E 2 = 1,02 x a , R 2

Logo, substituindo os valores, temos,

100 * 0,0099 + 50 * 0 = 100 * x a , R 2 + 50 * 1,02 * x a , R 2

x a , R 2 = 0,0066

Passo 3

Agora precisamos analisar o ponto de mistura para ver o que entra no terceiro estágio.

R 1 x a , R 2 + F 2 x a , F 2 = R m i s t x a , R m i s t

Logo, substituindo os valores, temos,

100 * 0,0066 + 70 * 0,005 = 170 * x a , R m i s t

x a , R m i s t = 0,0059

E para o terceiro estágio temos o seguinte balanço,

R m i s t x a , R m i s t + S x a , S = R 3 x a , R 3 + E 3 x a , E 3

Como R 3 e E 3 são correntes em equilíbrio,

x a , E 3 = 1,02 x a , R 3

Logo, substituindo os valores, temos,

170 * 0,0059 + 50 * 0 = 170 * x a , R 3 + 50 * 1,02 * x a , R 3

x a , R 3 = 0,0046

Passo 4

Por fim, para o 4 º e último estágio temos,

R 3 x a , R 3 + S x a , S = R 4 x a , R 4 + E 4 x a , E 4

Como R 4 e E 4 são correntes em equilíbrio,

x a , E 4 = 1,02 x a , R 4

Logo, substituindo os valores, temos,

1 7 0 * 0,00 46 + 50 * 0 = 1 7 0 * x a , R 4 + 50 * 1,02 * x a , R 4

x a , R 4 = 0,0 035

Agora para encontrar a fração mássica de dioxano basta substituir na equação de equilíbrio,

x a , E 4 = 1,02 * 0,0035

x a , E 4 = 0,0036

Resposta

x a , R 4 = 0,0035

x a , E 4 = 0,0036

Exercício Resolvido #8

Adaptado - Questão 1, 7ª Lista de Exercícios – Operações unitárias III Extração Líquido-líquido, UERJ

(Wankat, 3 ed. – Cap. 13 – D2) Deseja-se extrair uma solução diluída de proteína de uma solução aquosa de 5 % em massa de poli(glicol etilênico) (PEG) utilizando uma solução aquosa de 10 % em massa de dextrano. Sistemas de extração com duas fases aquosas são utilizados para recuperação de proteínas pois evitam a desnaturação da proteína, já que ambas as fases são aquosas. As duas fases podem ser consideradas imiscíveis.

A fase com dextrano é mais densa e será o solvente. A vazão da alimentação é de 20     k g / h e a vazão de solvente é de 20   k g / h , escoando em contracorrente com a alimentação em 2 estágios.

O coeficiente de distribuição de proteína é K d   = (fração mássica de proteína em PEG, x )/(fração mássica de proteína em dextrano, y ) =   0,12 Qual a recuperação total de proteína na fase de solvente?

Passo 1

Faaaala aíi, tudo beleza? Nessa questão nós precisamos encontrar a recuperação total de proteína na fase de solvente considerando sistemas de extração com duas fases aquosas. Para isso, temos dois estágios conforme demostrando abaixo:

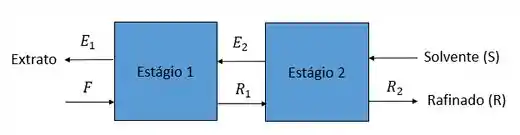
Onde,

K d   = 0,12

Passo 2

Para encontrar a recuperação total de proteína na fase de solvente precisamos inicialmente fazer um balanço de massa começando pelo primeiro estágio,

x a , F F + x a , E 2 E 2 = x a , E 1 E 1 + x a , R 1 R 1

Pelo coeficiente de distribuição temos,

x a , R 1 = x a , E 1 K d

Logo,

x a , F F + x a , E 2 E 2 = x a , E 1 ( E 1 + K d R 1 )

Passo 3

Fazendo um balanço agora para o segundo estágios temos,

x a , R 1 R 1 + x a , S S = x a , E 2 E 2 + x a , R 2 R 2

Pelo coeficiente de distribuição temos,

x a , R 2 = x a , E 2 K d

Logo,

x a , R 1 R 1 + x a , S S = x a , E 2 E 2 + K d R 2

x a , E 2 = x a , R 1 R 1 + x a , S S E 2 + K d R 2

Passo 4

Substituindo a última expressão do passo 2 na última expressão do passo 3 temos,

x a , F F + x a , R 1 R 1 + x a , S S E 2 + K d R 2 E 2 = x a , E 1 ( E 1 + K d R 1 )

Sabendo que,

x a , S = 0

F = R 1 = R 2 = E 1 = E 2 = S = 20

Podemos substituir os valores e obter,

x a , F * 20 + 0,12 * 20 + x a , S S 20 + 0,12 * 20 * 20 = x a , E 1 ( 20 + 0,12 * 20 )

x a , E 1 = 0,9872 * x a , F

Passo 5

Assim, a recuperação pode ser obtida por,

R e c u p e r a ç ã o = x a , F F - x a , R 2 R 2 x a , F F = x a , F F x a , F F - x a , R 2 R 2 x a , F F = 1 - x a , R 2 R 2 x a , F F

Manipulando as equações e substituindo os valores temos,

x a , R 2 0,12 = 0,12 * 0,9872 * x a , F * 20 20 + 0,12 * 20

x a , R 2 = 0,01269 * x a , F

Logo, a recuperação é:

R e c u p e r a ç ã o = 1 - 0,01269 * x a , F x a , F = 0,9873

Resposta

R e c u p e r a ç ã o = 0,9873