Difusão mássica
Produzido por Marcelo AlvesTeoria
Motivação
Fala aiii, tudo show de bola? Vamos já com um exemplo de difusão mássica para entendermos o conceito. Considere uma caixa na qual temos duas espécies gasosas diferentes, A e B, nas mesmas temperatura e pressão, que estão inicialmente separadas por uma divisória.
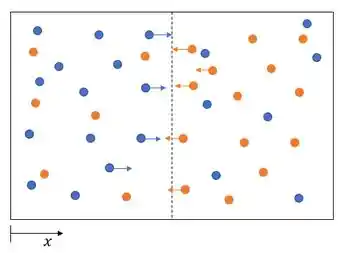
Se a divisória for removida, as duas espécies serão transportadas por difusão. Uma maior concentração significa mais moléculas por unidade de volume e a concentração da espécie A (azul) diminui com o aumento da distância . Enquanto a concentração de B (laranja) aumenta com .
A difusão mássica ocorre no sentido da diminuição de concentração. Sendo assim, há transporte líquido da espécie A para a direita e da espécie B para a esquerda.
Depois de um tempo suficiente grande, são atingidas concentrações uniformes de A e B, e não há transporte líquido da espécie A ou da espécie B através da caixa. Todo mundo fica equilibrado e nos encontramos em regime estacionário!
Considerações
Antes de seguir com o nosso estudo precisamos fazer algumas considerações para trabalhar com as equações. Essas premissas/considerações são:
- Em cada fase tem apenas dois componentes (A+B). Onde a molécula A é o soluto de interesse;
- Regime estacionário;
- Em cada face, a concentração total, C, é uniforme
- Geometria cartesiana
- Transferência de massa (TM) unidimensional na direção .
Fluxos de Transferência de Massa
Uma expressão importante para difusão mássica é a equação da taxa para a difusão mássica expressa pela lei de Fick. Na qual indica a transferência da espécie A em uma mistura binária de A e B. Ela pode ser escrita na forma vetorial como:
Agora vamos analisar cada integrante dessa equação mais de perto!

e (unidade ) são os fluxos difusos de “A” e “B” medidos na visão de um observador movimentando-se com a corrente. Ou seja, o observado está acompanhando juntinho essa transferência mássica acontecer.
e (unidade ou ) são as difusividades de “A” em “B” e de “B” em “A”.
E por fim,
Ah, e aqui a unidade de e vai ser beleza?
Show, agora bora exercitar!!
Considerações
Fluxos de Transferência de Massa
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
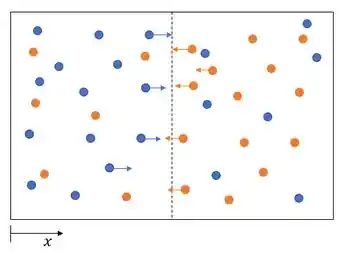
Considere uma caixa na qual temos duas espécies gasosas diferentes, A e B, nas mesmas temperatura e pressão, que estão inicialmente separadas por uma divisória. O que acontecerá se a divisória for removida?
Passo 1
Heyyy, tudo bem? Nessa questão nós temos uma caixa com duas espécies gasosas diferentes, A e B, nas mesmas temperatura e pressão separadas por uma divisória. E precisamos identificar o que acontece quando tiramos essa divisória.
Passo 2
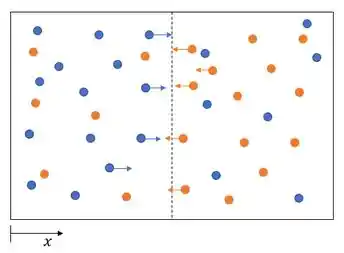
Ao tirar essa divisória iremos ter uma difusão mássica, ou seja, as partículas A e B vão ir de um lado para o outro da caixa.
A difusão mássica ocorre no sentido da diminuição de concentração. Sendo assim, há transporte líquido da espécie A para a direita e da espécie B para a esquerda.
Depois de um tempo suficiente grande, são atingidas concentrações uniformes de A e B, e não há transporte líquido da espécie A ou da espécie B através da caixa. Todo mundo fica equilibrado e nos encontramos em regime estacionário!
Resposta
Irá ocorrer a difusão mássica no sentido da diminuição de concentração. Sendo assim, há transporte líquido da espécie A para a direita e da espécie B para a esquerda.
Exercício Resolvido #2
Elaboração própria
Quais são as principais considerações que devemos assumir no processo de difusão mássica?
Passo 1
Fala aiii, tudo beleza? Nós vimos que o processo de difusão mássica ocorre no sentido da diminuição de concentração e queremos saber quais são as considerações que devemos assumir para que esse processo ocorra.
Passo 2
Para realizar o processo de difusão mássica amos assumir que:
- Em cada fase tem apenas dois componentes (A+B). Onde a molécula A é o soluto de interesse;
- Regime estacionário, ou seja, não muda com o tempo;
- Em cada face, a concentração total, C, é uniforme;
- Geometria cartesiana;
Resposta
- Em cada fase tem apenas dois componentes (A+B). Onde a molécula A é o soluto de interesse;
- Regime estacionário;
- Em cada face, a concentração total, C, é uniforme
- Geometria cartesiana
Exercício Resolvido #3
Lista de exercícios – Difusão, FUNDAÇÃO EDUCACIONAL ROSEMAR PIMENTEL CENTRO UNIVERSIT ÁRIO GERALDO DI BIASE INSTITUTO DE CIÊNC. EXATAS, DA TERRA E ENG . CURSO DE ENGENHARIA MECÂNIC A
Explique sucintamente os conceitos de regime estacionário e não estacionário na medida em que se aplica à difusão .
Passo 1
Heyyy, tutubom? Nessa questão nós queremos a influência do regime estacionário e não estacionário em relação à difusão.
Passo 2
O regime estacionário é a condição onde a taxa de transferência de uma determinada área não varia ao longo do tempo e pode ser aplicada ao fluxo de difusão através de uma superfície, conforme a lei de Fick .
Passo 3
Já no regime não estacionário, o fluxo de difusão e o gradiente de concentração em um ponto especificam no interior de um sólido variam o longo do tempo resultando num acumulo ou esgotamento líquido do componente que se encontra em difusão.
Resposta
O regime estacionário é a condição onde a taxa de transferência de uma determinada área não varia ao longo do tempo e pode ser aplicada ao fluxo de difusão através de uma superfície, conforme a lei de Fick .
No regime não estacionário, o fluxo de difusão e o gradiente de concentração em um ponto especificam no interior de um sólido variam o longo do tempo resultando num acumulo ou esgotamento líquido do componente que se encontra em difusão.
Exercício Resolvido #4
Concurso: Ministério Público da União (MPU) 2015, Cargo: Analista do MPU - Àrea de Atividade: Perícia - Especialidade: Engenharia Química
Acerca dos processos físicos que ocorrem por difusão de massa, julgue os itens seguintes. De acordo com a lei de Fick de difusão binária unidimensional, a estimativa do fluxo mássico de uma substância é obtida pela soma do fluxo volumétrico ponderado (bulk motion) com o valor de difusão molecular dessa substância.
- Certo
- Errado
Passo 1
Falaaaa aíi, tudo suave na nave? Nessa questão estamos falando sobre a lei de Fick de difusão, que tem a seguinte equação,
E ele está nos perguntando se a estimativa do fluxo mássico de uma substância é obtida pela soma do fluxo volumétrico ponderado (bulk motion) com o valor de difusão molecular dessa substância.
Passo 2
A unidade do fluxo mássico é e de vai ser . Como a unidade de volume é perceba que podemos manipular a equação de modo a usar o volume sim. Logo, a afirmativa é correta.
Resposta
- Certo
Exercício Resolvido #5
Exemplo 14.1, Fundamentos de transferência de calor e de massa, Frank P. Incropera
Considere a difusão de hidrogênio (espécie A) em ar, água líquida ou ferro (espécie B), a . Calcule os fluxos da espécie nas bases molar e mássica, se o gradiente de concentração em um local específico for igual a Calcule a taxa para a difusão mássica sabendo que a fração molar do hidrogênio,, é muito menor do que um e que .
Passo 1
Heyyy, tudo bem? Nessa questão nós queremos calcular o fluxo mássico, ou seja,
E para isso temos,
Passo 2
Substituindo os valores na equação temos,
Resposta
Exercício Resolvido #6
Exemplo 6.1.1, Processos de transporte y operaciones unitárias, 3ª edição, C.J. Geankoplis
Um tubo contém uma mistura de gás e a e de pressão total, constante em todo o comprimento do tubo. Em uma extremidade deste ponto 1, a pressão parcial de é de e na outra extremidade, a . Calcule em unidades SI e o fluxo específico de em estado estacionário quando o valor da mistura é . Use unidades SI e .
Passo 1
Oi oi oii, tudo show de bola? Nessa questão nós temos um tubo com uma mistura de gás e nas seguintes condições:
E as seguintes pressões em cada extremidade,

Com isso queremos, em unidades SI e o fluxo específico de em estado estacionário quando,
Passo 2
Como a pressão total é constante, então também é constante, e vamos ter o seguinte para um gás que atende à lei dos gases ideais:
Onde a unidade de é em de A mais B, o volume em , é a temperatura em e é ou e é . Em unidades cgs, R é .
Passo 3
Em estado estacionário, o fluxo , é constante. Além disso, o valor de um gás também é constante. Vimos que,
Escrevendo isto de outra forma temos,
Passo 4
Com base na lei do gás ideal,
Substituindo na equação do passo anterior temos,
Substituindo os valores dados no enunciado ficamos com,
Passo 5
Usando as pressões em atmosferas, com unidades SI,
Para unidades cgs, substituindo na equação,