Difusão mássica – Contradifusão Equimolar (CE)
Teoria
Motivação
Faaaaaaaaaaala ai!! Bora entender esse conceito aqui de contradifusão equimolar, que é um nome meio estranho, concorda?
Este fenômeno ocorre quando a condensação e evaporação de espécies químicas distintas, mas de características físicoquímicas semelhantes ocorrem ao mesmo tempo. Como por exemplo benzeno (A) e tolueno (B).
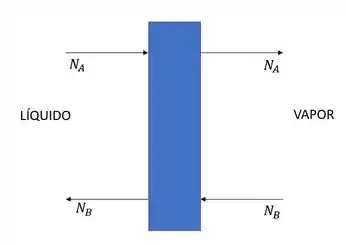
Então para cada mol de tolueno condensado, um mol de benzeno evapora.
Mas antes de ver as equações que essa situação implica, precisamos analisar o contexto.
Fluxo de Transferência de Massa na visão de um observador parado
A gente viu como funciona a transferência de massa como se o observador estivesse acompanhando junto a situação de perto, movimentando-se com a corrente, certo? Mas e se esse observador estivesse quieto e parado olhando tudo, como vai ser?
Nesse caso vamos ter o seguinte,
E olha só que bacana o que acontece quando nós somamos essas duas equações.
Sendo que,
Então ficamos com,
Tá, mas...
Bom, isso implica que,
O que facilita nossa vida, pois só precisamos utilizar uma daquelas expressões iniciais 😉
Contradifusão equimolar (CE)
Nós agora temos uma equação e duas varáveis . Então, precisamos de mais uma equação para fechar o grau de liberdade, beleza? E essa última relação nós vamos chamar de relação de determinância.
Ou,
Ahhh e é legal saber que essa análise é super utilizada em operações de destilação 😊
Agora vamos praticar o que aprendemos! \o/
Fluxo de Transferência de Massa na visão de um observador parado
Contradifusão equimolar (CE)
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Explique o conceito de contradifusão equimolar.
Passo 1
Heyyy, vamos começar os exercícios já falando sobre o conceito de contradifusão equimolar, beleza?
Passo 2
Este fenômeno ocorre quando a condensação e evaporação de espécies químicas distintas, mas de características físicoquímicas semelhantes ocorrem ao mesmo tempo. Como por exemplo benzeno (A) e tolueno (B).
Então para cada mol de tolueno condensado, um mol de benzeno evapora. 😉
Resposta
Este fenômeno ocorre quando a condensação e evaporação de espécies químicas distintas, mas de características físicoquímicas semelhantes ocorrem ao mesmo tempo.
Exercício Resolvido #2
Elaboração própria
Prove que para o fluxo de Transferência de Massa na visão de um observador parado.
Passo 1
Faaaaala aíii, tudo de boas? Nessa questão nós precisamos provar que,
Para o fluxo de Transferência de Massa na visão de um observador parado. Ou seja, nessa situação precisamos demonstrar que as difusividades são o inverso da outra.
Passo 2
No caso em que o observador está parado temos,
Somando essas duas equações,
Sendo que,
Passo 3
Então ficamos com,
Cortando de um lado com o outro temos,
Logo,
O que implica em uma difusividade ser o inverso da outra! 😊
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Questão 30, INEP - 2005 - ENADE - Engenharia - Grupo IV
Para uma mistura gasosa binária A+B, o fluxo molar do componente na direção () pode ser calculado pela expressão
Nessa equação, o primeiro termo do lado direito do sinal de igualdade representa a contribuição da transferência de massa por difusão (molecular e turbulenta), e o segundo, o fluxo convectivo total em relação a um ponto estacionário. No caso de contradifusão equimolar, . Assim, a equação pode ser simplificada para sendo o coeficiente de transferência de massa experimental. Para difusão de A através de B estagnante, não difundindo, . Nesse contexto, assinale a opção incorreta.
- Os coeficientes de transferência de massa para contradifusão equimolar e através de B estagnante são diferentes na equação
- As equações de transferência de massa para gases e líquidos são as mesmas, expressando-se os coeficientes em unidades apropriadas para cada caso.
- O coeficiente de transferência de massa a partir de um sólido pouco solúvel pode ser determinado submetendo-se esse material a um fluxo de solvente por determinado período de tempo, medindo-se a massa perdida e aplicando-se a equação A simplificada de .
- A velocidade de agitação, ou de escoamento, tem pouco efeito sobre o coeficiente de transferência de massa, o que justifica o fato de não haver parâmetros relacionados a ela nas equações apresentadas.
- No caso de acidente ambiental localizado que envolva contaminação em um ponto das margens de um lago com resíduo sólido, o conhecimento do equilíbrio de solubilidade é um dos elementos necessários para avaliação do impacto ambiental.
Passo 1
Ooi oii, turubom?! Nessa questão nós vamos falar sobre o fluxo molar e suas variações com algumas especificações. E precisamos encontrar a alternativa que possui a afirmativa incorreta. Então vamos analisar cada uma delas!
Passo 2
- Os coeficientes de transferência de massa para contradifusão equimolar e através de B estagnante são diferentes na equação
- As equações de transferência de massa para gases e líquidos são as mesmas, expressando-se os coeficientes em unidades apropriadas para cada caso.
- O coeficiente de transferência de massa a partir de um sólido pouco solúvel pode ser determinado submetendo-se esse material a um fluxo de solvente por determinado período de tempo, medindo-se a massa perdida e aplicando-se a equação A simplificada de
- A velocidade de agitação, ou de escoamento, tem pouco efeito sobre o coeficiente de transferência de massa, o que justifica o fato de não haver parâmetros relacionados a ela nas equações apresentadas.
- No caso de acidente ambiental localizado que envolva contaminação em um ponto das margens de um lago com resíduo sólido, o conhecimento do equilíbrio de solubilidade é um dos elementos necessários para avaliação do impacto ambiental.
Essa está correta, pois na contradifusão equimolar,
Logo,
Passo 3
Essa está correta, pois as equações de transferência de massa vão ser iguais para os fluidos!
Passo 4
Essa está errada!! Pois, o coeficiente de transferência para sólidos é diferente dos fluídos que vemos na disciplina sobre transferência de massa.
Passo 4
Essa está correta. Pois, a velocidade de fato não influencia.
E por fim,
Essa também está . Pois, precisamos saber o quanto de material contaminante foi dissolvido na água para escolher qual tratamento utilizar.
Resposta
Letra C
Exercício Resolvido #4
Enade 2014 – Questão 33
Para determinar a taxa molar total da mistura gasosa binária (A+B) deve-se somar as contribuições da transferência de massa por difusão e da transferência de massa por convecção em relação a um ponto estacionário, como apresentada na equação à seguir:
Sendo o coeficiente difusivo, a concentração total e a fração molar do gás A.
Nesse contexto, avalie as afirmações à seguir.
- Quando há contradifusão, a equação simplifica-se para .
- Considerando apenas a direção z, o fluxo molar de um componente numa dada fronteira pode ser calculado com a integração da equação apresentada no enunciado.
- A segunda lei de Fick é o resultado da simplificação da equação da continuidade mássica, considerando o regime transiente, a velocidade do meio nula, a temperatura e pressçao constantes e a ausência de reação química no meio onde ocorre o fenômeno de transferência de massa por difusão.
É correto o que se afirma em
- I, apenas.
- III, apenas.
- I e II, apenas.
- II e III, apenas.
- I, II e III.
Passo 1
Fala aíii, tudo bem? Nessa questão nós temos algumas afirmações a respeito da taxa molar que queremos identificar quais afirmações são verdadeiras. Então vamos lá!
Passo 2
- Quando há contradifusão, a equação simplifica-se para .
- Considerando apenas a direção z, o fluxo molar de um componente numa dada fronteira pode ser calculado com a integração da equação apresentada no enunciado.
- A segunda lei de Fick é o resultado da simplificação da equação da continuidade mássica, considerando o regime transiente, a velocidade do meio nula, a temperatura e pressçao constantes e a ausência de reação química no meio onde ocorre o fenômeno de transferência de massa por difusão.
Essa afirmação seria verdadeira estivéssemos avaliando uma contradifusão equimolar, ou seja, o numero de moles que se deslocam de cada componente devem ser iguais para que
Assim,
Seria simplificado para,
Como o enunciado não diz nada a respeito, não podemos considerar a afirmativa verdadeira.
Agora vamos analisar a afirmação II:
Passo 3
Avaliando a nossa equação temos,
Manipulando os termos, chegaríamos na expressão:
Daqui, teríamos que achar uma relação estequimétrica entre e , para que pudéssemos enfim passar esse da esquerda pra direita.
Assim, teríamos de um lado e do outro. Passando aquele pra esquerda, finalmente poderíamos integrar em relação à um z específico e encontrar o fluxo molar. Logo, a afirmação é verdadeira!
Passo 4
Por fim, temos:
A segunda Lei de Fick tem essa cara aqui:
Ela vem do balanço de massa diferencial, quando consideramos o fluido incompressível (ou seja, temperatura e pressão constantes, já que falamos de uma mistura de gases), sem reação química e sem escoamento. Logo, a afirmação está correta!
Resposta
Letra D.
Exercício Resolvido #5
Transferência de Massa, Eng Química Sanos SSP
Em um tubo de de comprimento há difusão de amônia gasosa (A) em nitrogênio () gasoso (B) a de pressão a No ponto 1 a pressão é de e no ponto 2 a pressão é de , e a difusividade é
Dado: Constante
a) Calcule o fluxo específico em estado estacionário
b) Calcule o fluxo específico em estado estacionário
Passo 1
Heyyy, nessa questão nós queremos encontrar o fluxo específico de A e B em um tubo de de comprimento que há difusão de amônia gasosa (A) em nitrogênio () gasoso (B). As condições do sistema são:
Onde,
Além disso, temos,
Passo 2
Calculando inicialmente o fluxo específico em estado estacionário temos,
Também podemos reescrever essa equação da seguinte forma,
Substituindo os valores temos,
Passo 3
Para fazer o mesmo com B precisamos primeiro encontrar as pressões parciais de B. Como o enunciado nos deu a pressão total, podemos calcular as pressões parciais da seguinte forma,
E para o segundo ponto temos,
Passo 4
Calculando agora o fluxo específico em estado estacionário temos,
Substituindo os valores temos,
Como o valor de deu negativo, isso significa que o fluxo vai do ponto 2 para o ponto 1.