Método Mc-Cabe Thiele Analítico
Produzido por Marcelo AlvesTeoria
Método Mc-Cabe Thiele Analítico
O Método Mc-Cabe Thiele Analítico, ao invés de utilizar o gráfico para traçar os estágios, utiliza equações para determinar as composições de equilíbrio dos estágios.
Equação do Método Mc-Cabe Thiele Analítico
A Equação do Método Mc-Cabe Thiele Analítico que resume todos os tipos de seções que podem aparecer na coluna é essa aqui:
Onde são as seções da coluna e é a seção de absorção. Já o termo resume as variações que podem ocorrer em cada seção, tipo entradas e saídas. Então, para a gente poder calcular as composições de equilíbrio, vazões e todas as seções, podemos montar uma tabelinha para facilitar nossa vida:
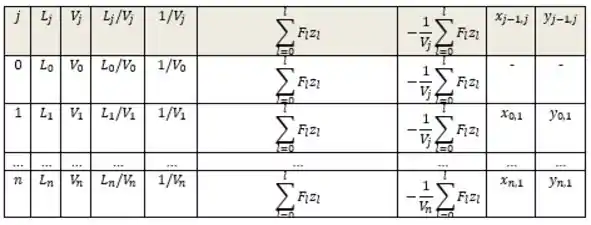
E como calculamos as duas últimas colunas dessa tabela? Vamos utilizar as fórmulas abaixo que vieram das deduções de balanço de Massa.
Sendo que assim se a carga/retirada daquela seção for líquido saturado, por exemplo, você só precisa calcular . Por outro lado, para cargas/ retiradas vapor saturado, só precisamos calcular o .
Lembrando também que as relações que vimos entre e que deixam um mesmo estágio, ou seja, estão em equilíbrio continuam válidas.
Obs: Alguns professores deixam utilizar excel na prova, então levar a tabela com as equações já preenchidas ajuda muito a ganhar tempo 😊
Razão de Refluxo Mínima
No método Mc-Cabe Thiele analítico, a Razão de Refluxo Mínima vai ser dada por:
Onde é a composição do produto de topo e e são as composições de vapor e líquido da carga. Lembrando que para cargas bifásicas, a relação das composições fica:
Análise do Sistema de Topo e de Fundo
No método Mc-Cabe Thiele analítico, quando informarem que o condensador é total, você já pode escrever de cara que . Aí, é só seguir aplicando as fórmulas da tabelinha que mostramos a partir desse que obtivemos. No entanto, se o condensador for parcial, a relação entre e dependerá do equilíbrio.
Já o sistema de fundo sempre vai ser o produto saindo como líquido saturado, ou seja, sempre teremos um saindo. No entanto, mesmo assim, ainda podemos ter um refervedor total ou parcial. No caso de um refervedor total, . Já para o refervedor parcial, precisaremos calcular o equilíbrio assim como comentamos para o condensador parcial, ok?
Eu super sei que isso tudo parece muito confuso. Então vamos para os exercícios que vamos ver como resolver isso tudo com exemplos, ok?