Método de Ponchon - Savarit
Teoria
Detalhes Gerais do Método
Nós vimos que o Método Mc-Cabe Thiele era um método aproximado, certo? O Método de Ponchon -Savarit, por sua vez, é um método preciso. O motivo dessa precisão é que ele considera tanto o Balanço de Massa, quanto o Balanço de energia. E nesse método não temos uma versão analítica, ele é puramente gráfico!
Para isso, vamos utilizar muitos gráficos de entalpia em função da composição, ok? Bora ver como utilizar esse método para achar o número de estágios da nossa coluna???
Método Ponchon - Savarit
Vamos começar analisando uma coluna de destilação com uma seção de absorção e outra de esgotamento, ok?
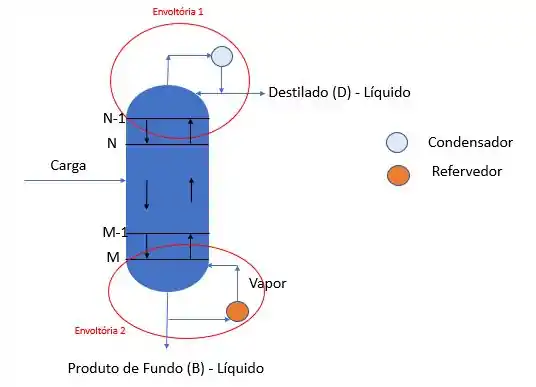
Nós podemos fazer um balanço de energia no topo e no fundo das colunas marcadas para conseguirmos entender como o método Ponchon-Savarit funciona, ok?
Para isso, vamos definir que é a entalpia dos vapores e será usado para entalpia de líquido. Os índices são usados para indicar de qual estágio está saindo aquela corrente.
Para o Balanço de energia da envoltória 1, obtemos a seguinte equação, considerando que é o calor do condensador e não precisa ser multiplicado por nenhuma vazão de corrente, ok? já possui a mesma unidade da entalpia vezes a vazão, então não tem problema nenhum nessa equação 😊
Podemos reorganizar nossa equação para ficar com essa carinha aqui:
Depois, para a envoltória 2, podemos fazer novamente o balanço de massa, só que a envoltória 2 engloba o refervedor. Então, ao invés de vamos utilizar .
Reorganizando a equação, obtemos que:
Nas questões de Ponchon-Savarit, para não nos confundirmos, precisamos estar sempre conferindo as unidades. Nesse caso, podemos fazer a seguinte análise de unidades:
Esses termos e serão substituídos por apenas uma letra, que é geralmente a que aparece nas aulas, para simplificar as equações, beleza?
Podemos fazer uma simplificação de notação maior ainda para facilitar nossa vida, ok?
E, se a gente organizar direitinho, podemos usar esses deltas que mostramos agorinha para simplificar o balanço de energia da nossa coluna completa.
Aplicações no gráfico
Beleza, eu falei de váaaarias equações até agora , mas lá no início falei para vocês que o Ponchon era um método gráfico, certo? Como relacionar isso tudo com gráficos?
Bem, a importância dessas equações é que elas serão as equações das retas que traçaremos no gráfico para determinar o número de estágios da coluna. Podemos citar alguns exemplos com equações que já deduzimos:
Linha de operação na seção de absorção:
Linha de operação na seção de esgotamento:
Linha de Balanço global:
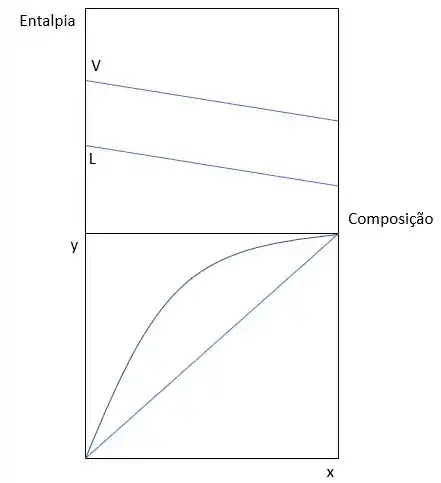
Geralmente, nós receberemos os gráficos bem parecidos com a representação abaixo. Na parte superior do gráfico, vemos a entalpia em função da composição. A entalpia pode ser de líquido (linha inferior) ou de vapor (linha superior). Entre elas, existe a região de líquido e vapor. Já no gráfico de baixo, temos apenas a representação do diagrama x-y que irá ser essencial para terminarmos esses exercícios.
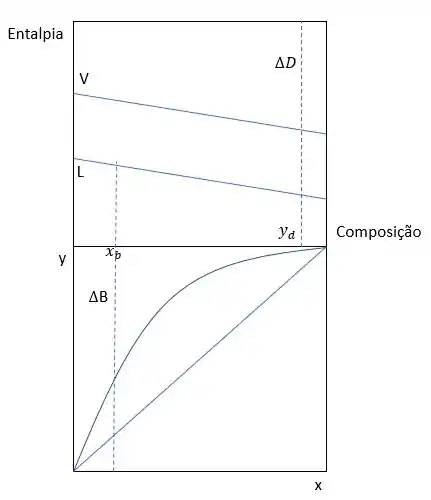
Em seguida, precisaremos marcar as composições dos produtos de topo e de fundo. Nesse caso, do exemplo, estamos considerando que o produto de topo é vapor saturado e o de fundo é líquido saturado.
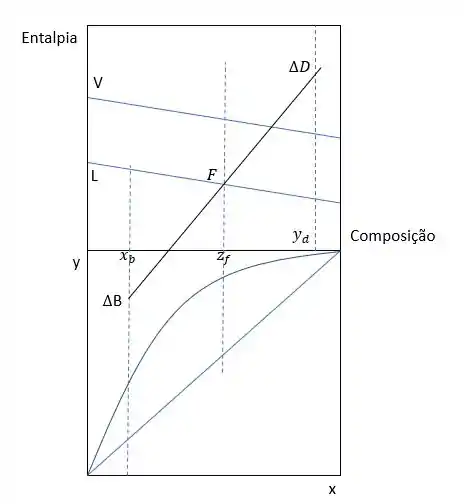
Além disso, se considerarmos, por exemplo, uma carga com composição e que seja um líquido saturado, podemos marcá-la na reta de entalpia de líquidos no gráfico. E, como vimos, a reta do balanço global é dada por , isso indica que são colineares, ou seja, pertencem a mesma reta. Então se conhecemos por exemplo o através de informações que foram fornecidas, podemos ligar ele e o , para encontrar o . O será a interseção da reta que traçamos com a composição de ( representada pelo tracejado na vertical).
Portanto, essa reta em preto que achamos representa o nosso balanço global. Qualquer reta que traçarmos entre o Balanço Global e a linha do será pertencente a seção de absorção. E as retas que traçarmos entre o Balanço Global e a linha do faz parte da seção de esgotamento.
Mas e como traçar essas retas? Bem, nós vamos descer lá da composição do vapor até tocar a curva de equilíbrio e ver a composição do líquido. Com isso, subimos novamente para o gráfico superior e traçar uma reta ligando esses dois pontos. Essa reta é a amarração entre o líquido e vapor em equilíbrio.
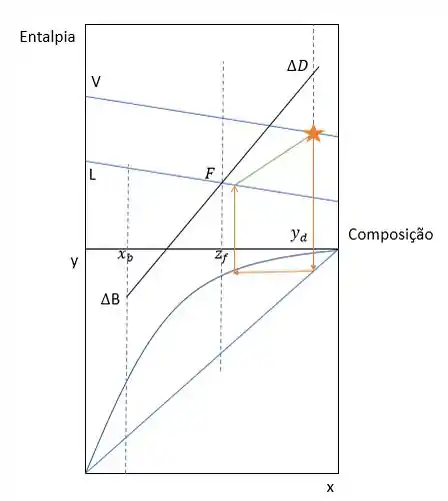
Em seguida, para ver a composição do vapor do próximo estágio, como ainda estamos na seção de operação, vamos traçar uma reta da composição do líquido que encontramos até o condensador e esse será nosso primeiro estágio (representado em vermelho).
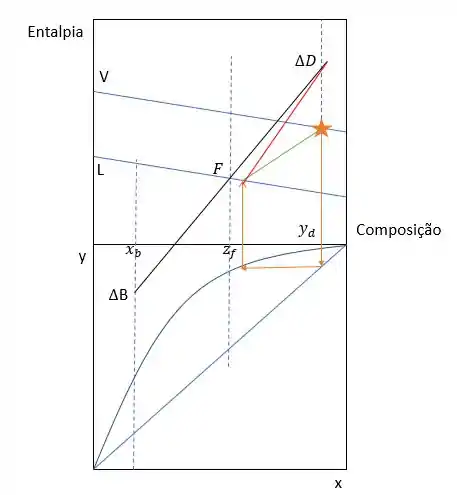
Novamente, vamos recorrer ao gráfico de equilíbrio para achar o líquido em equilíbrio com esse vapor. Esse procedimento vai se repetir, usando o condensador, até ultrapassar a linha de balanço global. A partir dessa linha, faremos a mesma coisa, mas usando como referência o refervedor, ou seja, conforme as linhas lilás. E qual vai ser a hora de parar? Quando a composição do produto de fundo for ultrapassada 😊
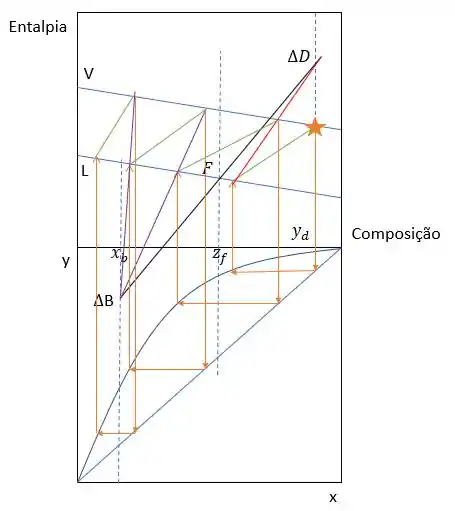
Eu sei que parece um gráfico todo rabiscado e no papel milimetrado fica ainda pior. Então, tentem sempre fazer o máximo de linhas possíveis usando lápis bem fraquinho e deixem para marcar colorida só as que facilitam para a sua visualização, ok?
E quantos estágios teóricos são necessários para essa coluna? Apenas 4, que são as nossas linhas verdes. E qual é o prato téorico de carga? Será aquele que cruza o nosso balanço global, portanto será o prato 2 ( lembrando que começamos a contar a partir do como prato 1)!
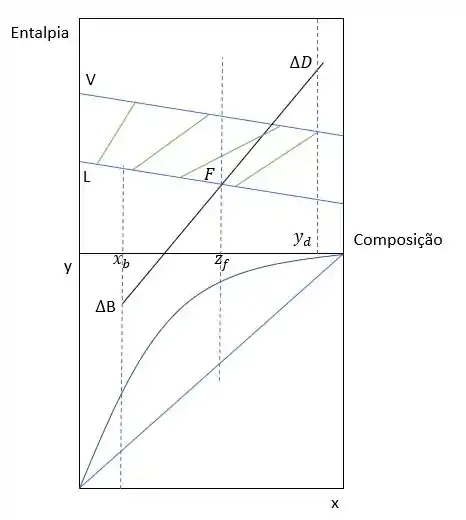
Então, nós vimos como determinar o número de estágios da coluna e também determinar o prato téorico de carga! 😊 Corre lá para os exercícios para praticarmos isso.... E se quiser ver mais um pouquinho sobre razão de refluxo nesse método e também como aplicar para outros tipos de colunas, bora lá para os próximos tópicos.
Aplicações no gráfico
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado – Concurso EAOT 2009 – Especialidade: Engenharia Química
Os métodos McCabe-Thiele e Ponchon-Savarit são comumente aplicados em problemas de projeto de colunas de destilação. Em relação a estes métodos, pode-se afirmar que:
A) O método McCabe-Thiele é um método rigoroso, que resolve formalmente os balanços de energia na coluna.
B) Os métodos McCabe-Thiele e Ponchon-Savarit têm premissas idênticas.
C) O método Ponchon-Savarit só pode ser aplicado em sistemas cuja fase líquida seja ideal.
D) O método McCabe-Thiele considera vazões molares constantes ao longo de uma seção da coluna de destilação.
Passo 1
Nessa questão é pedido que nós façamos uma análise comparativa de dois métodos super importantes para coluna de destilação que são McCabe-Thiele e Ponchon-Savarit. Sendo assim vamos analisar caso a caso.
Passo 2
Na letra A, a questão que o método McCabe-Thiele é um método rigoroso, que resolve formalmente os balanços de energia na coluna. Já vimos na teoria que isso não é verdade, pois para McCabe-Thiele podemos usar tanto método analítico, através de balanços como o método gráfico. Sendo assim, a alternativa é falsa.
Já a letra B, afirma que os métodos McCabe-Thiele e Ponchon-Savarit têm premissas idênticas. Vimos que o primeiro tem tanto o método analítico como gráfico, enquanto o segundo possui método apenas gráfico. Porém, ambos têm o objetivo de calcular o número de estágios necessários para a destilação. Logo, a alternativa é verdadeira.
Passo 3
Sendo assim, as alternativas C e D são falsas. Pois não é exigido que a fase líquida seja ideal para aplicação do método Ponchon-Savarit e o método McCabe-Thiele não considera vazões molares constantes ao longo de uma seção da coluna de destilação.
Resposta
Alternativa B
Exercício Resolvido #2
Elaboração própria
Analise o gráfico do método Ponchon-Savarit abaixo e identifique qual é o prato teórico de carga.
Passo 1
A questão nos impede para analisarmos através do gráfico qual é o prato teórico de carga. Sendo assim não precisamos acrescentar informações ao gráfico.
Passo 2
O prato teórico de carga, que é o estágio ideal de alimentação e o prato que cruza o balanço global. Assim, vemos que é o prato 2.
Resposta
Prato 2.
Exercício Resolvido #3
Elaboração própria
Analise o gráfico de Ponchon-Savarit abaixo e identifique quantos estágios são utilizados.
Passo 1
A questão nos impede para analisarmos através do gráfico a quantidade de estágios utilizados. Sendo assim não precisamos acrescentar informações ao gráfico.
Passo 2
O número de estágio é indicado pelas retas roxas, assim, como temos seis retas roxas temos seis estágios no total.
Repara que se a questão nos pedisse para informar qual é o prato teórico de carga, responderíamos que é o prato 3 pois é onde cruza o nosso balanço global.
Resposta
6 estágios.
Exercício Resolvido #4
Adaptado - Destilação, traçado de etapas de Ponchon-Savarit- Engenharia Química - UANL
Uma mistura líquida saturada de hexano e octano com é alimentada a uma coluna de destilação. Se deseja que o produto destilado tenha mol de hexano e o fundo . Encontre o número de estágios através do método Ponchon-Savarit sabendo que .
Passo 1
A questão nos forneceu o diagrama de equilíbrio e o gráfico de entalpia x composição para a mistura hexano e octano e nos pediu para calcularmos o número de estágios. Então vamos aplicar o que vimos na teoria para o método de Ponchon-Savarit.
Passo 2
Primeira coisa que vamos analisar é o gráfico de entalpia x composição (o primeiro). Repara que no gráfico tem traçado duas linhas cinzas. Essas linhas representam as linhas de fundo e topo da coluna, respectivamente.
É possível perceber, também através do enunciado pois ele nos informou que o produto destilado tema em mol de hexano e o fundo . Agora, vamos traçar a reta do nosso balanço global.
Passo 3
Para traçar a reta do nosso balanço global, vamos primeiro marcar no gráfico de entalpia x composição o valor de e de .
Agora, só precisamos ligar os pontos e prolongar a reta para termos nossa reta do balanço global.
Traçando a reta, encontramos também o valor de .
Passo 4
Agora, nós vamos descer lá da composição do vapor até tocar a curva de equilíbrio e ver a composição do líquido. Com isso, subimos novamente para o gráfico superior e traçar uma reta ligando esses dois pontos. Essa reta em verde é a amarração entre o líquido e vapor em equilíbrio e representa um estágio.
Passo 5
Em seguida, para ver a composição do vapor do próximo estágio, como ainda estamos na seção de operação, vamos traçar uma reta da composição do líquido que encontramos até o condensador e esse será nosso primeiro estágio (representado em vermelho).
Passo 6
Depois disso, vamos recorrer ao gráfico de equilíbrio para achar o líquido em equilíbrio com esse vapor. Esse procedimento vai se repetir, usando o condensador, até ultrapassar a linha de balanço global.
A partir dessa linha, faremos a mesma coisa, mas usando como referência o refervedor até que a composição do produto de fundo seja ultrapassada como vimos na teoria, beleza? E vamos ter como resultado final 5 estágios.
Resposta
5 estágios.
Exercício Resolvido #5
Adaptado – Lista de Operações Unitárias 1 – UFF – Professor Jorge
de uma mistura binária, contendo molar da espécie volátil e em seu ponto de bolha, devem ser separados em uma coluna de pratos que opera a e que possui um condensador total e um refervedor parcial. A coluna deve operar em regime permanente, gerando um destilado com molar da espécie leve e um resíduo molar dessa mesma espécie.
Utilizando o método de Ponchon-Savarit e os diagramas entalpia-composição e x-y apresentados na figura abaixo, responda qual o número teórico de estágios de equilíbrio necessários sabendo que e
Passo 1
O enunciado está nos pedindo para utilizar o método Ponchon-Savarit e encontrar o número teórico de estágios de equilíbrio. Para isso, nos forneceu o valor da vazão de entrada, que não vamos precisar utilizar, pois já temos os valores de e . Então, já podemos colocar essas informações no nosso gráfico.
Passo 2
No gráfico, nós vamos traçar a reta do balanço global marcando os pontos e , ou seja, e .
Passo 3
Agora, precisamos traçar as retas dos estágios com o auxílio do diagrama de equilíbrio seguindo os passos que vimos na teoria:
Passo 4
Vamos repetir o processo anterior até alcançar o ponto . Assim, vemos que número teórico de estágios de equilíbrio é .
Resposta
estágios.
Exercício Resolvido #6
Adaptado - Caderno de Operações Unitárias I – UFF – Professor Jorge
Sabendo que uma coluna de destilação é alimentada com de uma mistura com n-heptano e etilbenzeno, em seu ponto de bolha. Determine o número do estágio de ótima localização através do método Ponchon-Savarit.
Dado: , e
Passo 1
O enunciado está nos pedindo para determinar o número do estágio de ótima localização através do método Ponchon-Savrit e para isso nos forneceu os valores da vazão de alimentação de e os gráficos necessários. Então, devemos inicialmente fazer um balanço para encontrar e traçar nossa reta do balanço global.
Passo 2
Precisamos primeiro, encontrar as vazões da coluna de topo e de fundo. Então, vamos utilizar a seguinte expressão obtida pelo balanço mássico:
Substituindo os valores informados no enunciado temos:
Como,
Então,
Repara que aqui nós temos que usar o balanço mássico e não o balanço de energia, beleza?
Passo 3
Agora podemos calcular o valor de usando o balanço de energia, pois já temos o valor da vazão do fundo da coluna. Então,
Ou,
Substituindo os valores,
Passo 4
Finalmente podemos ir para o gráfico e traçar a reta do balanço global marcando os pontos e , ou seja, e .
Passo 5
Agora, só precisamos traçar as retas dos estágios com o auxílio do diagrama de equilíbrio seguindo os passos que vimos na teoria:
Passo 6
Vamos repetir o processo anterior até que o estágio cruze a nossa reta de operação. Assim, vemos que nossa localização ótima de alimentação é no estágio .
Resposta
Estágio .
Exercício Resolvido #7
Adaptado - Lista – Operações Unitárias II (UFRJ)
Assuma que as alimentações são líquidas saturadas e use as simplificações usuais. Faça o diagrama de entalpia X composição e o diagrama de equilíbrio (xy). Assuma que as curvas de vapor e líquido saturado são retas paralelas. A volatilidade de A em relação a B é constante e igual a . A é o componente mais volátil.
Passo 1
Essa questão é sobre Ponchon – Savarit e não temos nenhum gráfico dado. Portanto, precisaremos montar esses gráficos. Para isso, vamos começar com a curva de equilíbrio Líquido-Vapor.
Na questão, foi dado o alfa (), podemos manipular a expressão do alfa para calcular o em função do e vice versa. Portanto, éisso que faremos nessa questão 😊
Utilizando a fórmula acima, calculamos o para diferentes valores de .
Traçando o gráfico, obtemos algo com esse formato ( lembrando que precisamos traçar a diagonal).
Passo 2
O próximo gráfico que precisaremos traçar é o gráfico de entalpia. Para isso, a única informação que foi dada é que são duas retas paralelas e, portanto, vamos representar elas assim. Lembrando que a escala do eixo x para o gráfico de equilíbrio deve ser o mesmo do gráfico de entalpia.
Cada pessoa fazendo essa questão vai obter retas com inclinações diferentes. Portanto, os resultados podem variar um pouco, mas a forma de fazer a questão é a mesma.
Resposta
Exercício Resolvido #8
Lista – Operações Unitárias II (UFRJ)
Uma coluna que separa A e B tem duas alimentações com composições molares iguais a , vaporizada e , líquida saturada. As alimentações são introduzidas na proporção de moles na alimentação mais rica em A e moles na alimentação mais pobre em A. Quando a razão de refluxo é 3,0 a coluna produz um produto de topo com fração molar de A e um produto de fundo com 0,1 fração molar de A. Pergunta-se:
- Os estágios que devem ser colocadas as cargas;
- Quantos estágios serão necessários.
Passo 1
Essa questão é sobre Ponchon – Savarit e já nos foi fornecido o gráfico. Então, primeiro precisamos marcar os dados sobre as cargas e os produtos de topo e fundo. O produto de topo possui . Já as cargas ( 2 cargas) possuem as seguintes características:
sendo vaporizada
sendo líquida saturada
Quando temos duas cargas no método de Ponchon Savarit, precisamos calcular o .
No gráfico, marcamos com duas estrelas azuis. Marcando uma linha entre as duas cargas, marcamos o ponto que equivale ao em laranja.
Passo 2
Não temos nenhuma informação do produto de topo (produto D) e produto de fundo (produto B). Mas podemos utilizar a informação de Razão de Refluxo para calcular o .
Podemos marcar esse ponto no gráfico utilizando a diferença entre vapor e líquido (), essa diferença está marcada no gráfico.
Passo 3
Com esse ponto do condensador, podemos traçar a reta de balanço global passando pelo condensador, o ponto de carga médio () e depois chegando no refervedor, que pode ser determinado através da interseção da reta com o .
Passo 4
Depois disso, agora que os pontos do condensador e do refervedor estão marcados. Podemos traçar a reta do destilador até a carga 1 e do refervedor até a carga 2. Quando estivermos traçando os estágios, vamos usar essas retas como referência para saber quando precisamos trocar de ponto de referência entre as seções de absorção, esgotamento e intermediário.
Passo 5
Depois disso, como temos também seção intermediária, teremos , que será a interseção de absorção e de esgotamento. Essa interseção tá marcada de amarelo na figura abaixo.
Os estágios foram traçados conforme a figura a seguir e as retas em vermelho foram utilizadas para determinar os estágios da absorção. Em amarelo são as retas do estágios intermediário. Por fim, as retas verdes foram utilizadas para determinar o refervedor. É muiiito importante lembrar que precisamos também utilizar as curvas de equilíbrio para ver os e em equilíbrio.
Portanto, temos 5 estágios na coluna. Os estágios de carga são aqueles em que cortam as cargas. Portanto, são os estágios 2 e 3.
Resposta
5 estágios totais.
Estágios de carga são 2 e 3.