Fugacidade e Atividade no ELV
Produzido por Marcelo AlvesTeoria
Já vimos o que são fugacidade, atividade, seus coeficientes e as relações válidas entre esses caras.
Agora vamos estudar algumas relações que só são válidas no equilíbrio líquido-vapor, beleza?
São 4 relações e algumas simplificações que vão falicitar nossas vidas assim que um exercício trouxer as palavrinhas mágicas “equilíbrio líquido-vapor”. Bora lá!
Equilíbrio Líquido-Vapor – Relação 1
A gente já sabe que existe fugacidade tanto para líquido quanto para vapor. Mas quando estamos falando do líquido e do vapor em equilíbrio, como essas fugacidades se relacionam? Será que a fugacidade do vapor é maior do que a do líquido? Ou será que é menor?

Na verdade, se líquido e vapor estão em equilíbrio, eles terão a mesma fugacidade! Então:
Podemos relacionar essas fugacidades também através dos coeficientes de fugacidade (), pois:
Vapor:
Líquidos:
Isolando as fugacidades:
E, finalmente, igualando elas:
Simplificando a pressão que apareceu nos dois lados, obtemos:
Ih, mas repara só... Nós já conhecemos esse !!!! É o da constante de equilíbrio líquido- vapor!! Lembra?
Então podemos escrevê-lo em função dos coeficientes de fugacidade:
Isso significa que para um sistema multifásico conseguimos medir a constante de equilíbrio em função dos coeficientes. Chamaremos essa relação de Relação 1.
Equilíbrio Líquido-Vapor – Relação 2
Já vimos como a fugacidade se comporta no equilíbrio. Agora, bora ver como isso funciona para a atividade e o coeficiente de atividade. Dependendo da questão, pode ser que seja necessário utilizar ou um ou outro.
Vamos começar falando da fase vapor. Para essa fase, temos:
Se a gente manipular essas expressões da atividade, podemos obter o seguinte:
E podemos fazer exatamente a mesma coisa para a fase líquida. Assim, vamos obter que:
Como as fugacidades do líquido e vapor são iguais no equilíbrio, podemos igualar as duas eexpressões aí de cima e chegar em:
Reorganizando:
Ih, conseguimos outra forma de escrever nosso !
E essa vai ser a nossa Relação 2!
Dizemos que as Relações 1 e 2 são Relações Simétricas, por causa dessa semelhança entre o numerados e o denominador do .
Equilíbrio Líquido-Vapor – Relação 3
As próximas relações são apenas outras formas que podemos manipular as equações e obter as fugacidades da fase líquida e da fase vapor, como, por exemplo:
Então, novamente, se igualarmos as duas fugacidades:
E aí semprevamos organizar a equação para aparecer o termo , pois sabemos que ele é igual ao nosso .
Essa é a nossa Relação 3 e dizemos que ela é não simétrica (ou assimétrica), pois o denominador e numerador não são parecidos. Eles não seguem um padrãozinho igual nas relações 1 e 2.
Equilíbrio Líquido-Vapor – Relação 4
A nossa quarta e última relação parte das seguintes manipulações de fugacidade:
Igualando as duas fugacidades, já que estamos no equilíbrio líquido-vapor:
E essa é a nossa Relação 4, que também é assimétrica.
Todas as 4 relações são válidas para sistemas em altas e baixas pressões. Mas, em pressões baixas, é possível fazer algumas simplificações extras que vão facilitar nossa vida 😊
Simplificações para Baixas Pressões
Quando estamos falando de pressões baixas, ou seja, bem próximas à pressão atmosférica, a fase vapor possui o comportamento bem próximo de um gás ideal. Portanto, podemos dizer que nessas condições .
Outra simplificação que podemos fazer em decorrência disso é dizer que a fugacidade do líquido no estado padrão é basicamente igual a nossa pressão de vapor, ou seja:
Assim, podemos reescrever nossas relações e obter a seguinte simplificação:
Esse modelo só pode ser utilizado em baixas pressões (no máximo 50 atm).
E se as duas substâncias envolvidas forem bem parecidas, por exemplo da mesma série homóloga, podemos dizer que , pois temos uma solução líquida com comportamento ideal.
Presta atenção, hein... Quanto mais simplificações nós aplicamos, mais restrita fica a utilização da equação. Essa última aí, por exemplo, só é válida em: sistema líquido-vapor em equilíbrio, baixa pressão e substâncias similares.
Mas e quando o nosso coeficiente de atividade for diferente de 1 (), como vamos calculá-lo?
Cálculo do Coeficiente de Atividade
Bem, existem diversas formas de calcular o coeficiente de atividade, mas o jeito mais comum é o Modelo de Van Laar, que é empírico e utiliza duas constantes. Você também pode ouvir falar em Wilson, NRTL, UNIQUAC e etc...
Pelo Modelo de Van Laar:
Então a gente pode calcular o coeficiente de atividade para dois componentes (e ) de uma mistura binária. Maaaas, para isso, a gente precisa conhecer as duas constantes de quando esses componentes estão juntos ( e ). E isso nem sempre é possível ☹
Cálculo da Pressão de Vapor
Para o cálculo da pressão de vapor de misturas, geralmente usamos a equação de Antoine. Nessa equação, já temos as constantes tabeladas e a pressão crítica para diversos componentes, então fica bem mais simples de trabalhar!
Essa equação pode aparecer de várias formas, uma delas é essa:
Onde as pressões estão em e a temperatura deve ser usada em Fahrenheit. são constantes e é a pressão crítica.
As unidades vão variar de acordo com a tabela de dados que utilizarmos.
A outra forma que essa equação pode aparecer é:
O é a mesma coisa que o , beleza?
Então bora lá para os exercícios ver como podemos aplicar tudo isso!
Equilíbrio Líquido-Vapor – Relação 2
Equilíbrio Líquido-Vapor – Relação 3
Equilíbrio Líquido-Vapor – Relação 4
Simplificações para Baixas Pressões
Cálculo do Coeficiente de Atividade
Cálculo da Pressão de Vapor
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Calcule a pressão de saturação do benzeno. Considere válida a equação de Antoine e uma temperatura igual a .
Para os valores tabelados, utilize os recortes disponibilizados a seguir:
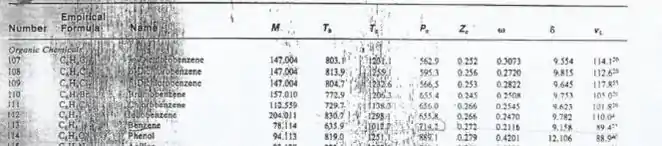
Passo 1
Precisamos calcular a pressão de saturação e o enunciado já nos dá qual equação utilizar: a equação de Antoine.
E quais seriam essas constantes , e ? Precisamos pegar os dados na tabela. Provavelmente, seu professor vai te dar uma tabela dessas, mas colocamos aí os recortes dela para facilitar! 😊 Bora procurar o benzeno:
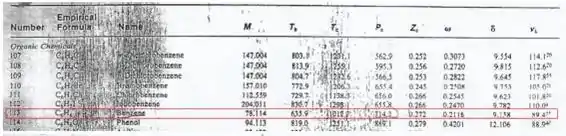
Olhando os dados, temos as seguintes informações para o benzeno:
Passo 2
Agora, o que precisamos é converter a temperatura, pois a informação foi dada em graus Celsius e queremos Fahrenheit. E vamos relembrar como fazer essa conversão:
Então, vamos substituir a nossa temperatura de .
Passo 3
Pronto, agora já temos tudo para jogar na fórmula:
A partir daí, conseguimos obter a pressão que desejamos 😊
Resposta
Exercício Resolvido #2
Elaboração própria
Determine a constante de equilíbrio líquido-vapor do iodo-benzeno a pressão atmosférica e . Considere o coeficiente de atividade igual a e utilize a relação:
Para pressão de saturação utilize a equação de Antoine.
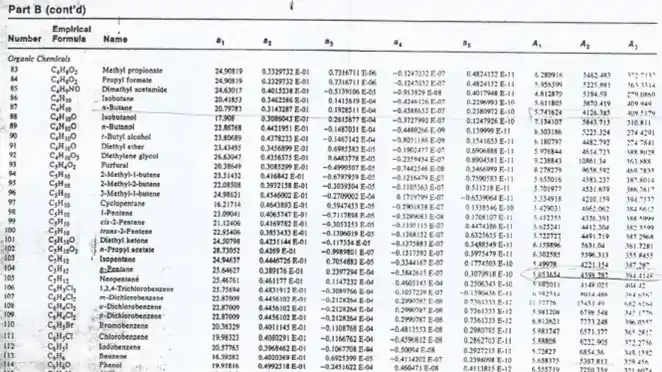
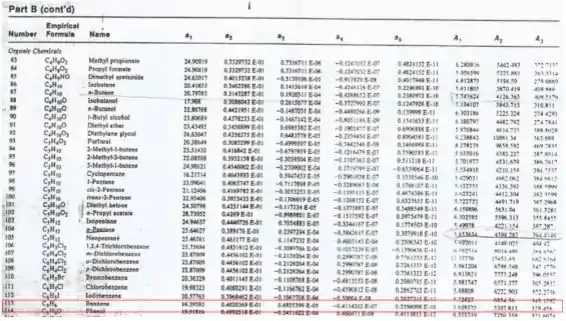
Para os dados tabelados, utilize os recortes disponibilizados a seguir:
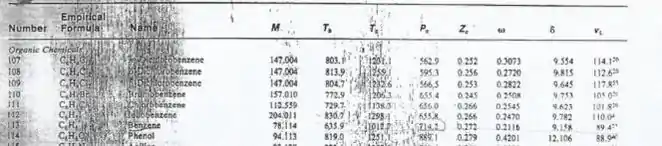
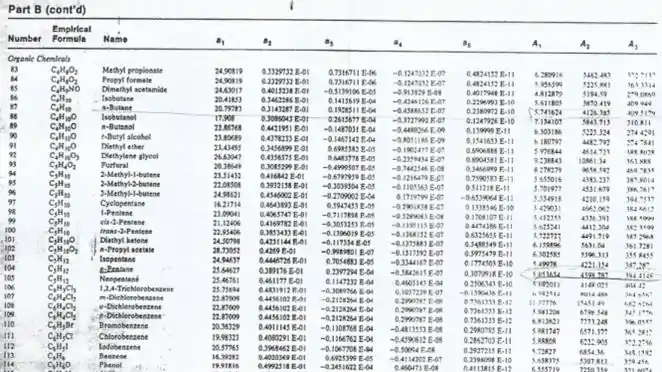
Passo 1
O nosso objetivo é calcular o . E para isso vamos usar a seguinte relação:
Pelo enunciado sabemos que e que a pressão do sistema é a pressão atmosférica. Logo:
Então, a única coisa que ficou faltando foi o , que vamos determinar pela equação de Antoine, já que . Beleza?
Passo 2
Pela equação de Antoine:
Bora pegar a pressão crítica e as constantes para o iodo-benzeno na tabela!
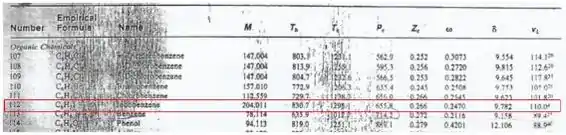
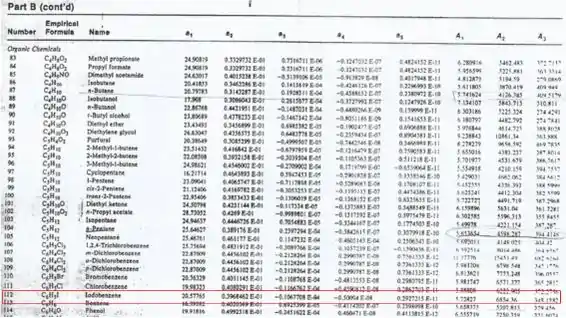
Olhando os dados, temos as seguintes informações para o iodo-benzeno:
Passo 3
Para a equação de Antoine usamos a temperatura em Fahrenheit. Então precisamos converter:
Passo 4
Pronto, agora já temos tudo para jogar na fórmula:
Passo 5
A última coisa que precisamos fazer é substituir a pressão de saturação na fórmula do com os outros dados que já tínhamos.
Pronto, agora chegamos na nossa resposta final 😊
Resposta
Exercício Resolvido #3
Adaptado de Lista Operações Unitárias II - UFRJ
A tabela abaixo apresenta as constantes da equação de Antoine sob a forma:
Para acetona e para o metanol.

Determine a pressão de uma solução aquosa de acetona e de metanol a .
Passo 1
Vamos começar pensando em tudo que precisamos fazer para resolver essa questão.
O enunciado pede pra calcular a pressão de um líquido que é uma mistura de dois componentes. Nesse caso, a expressão que utilizamos é:
Nós já conhecemos as frações molares (dadas no enunciado) e precisamos calcular as pressões de saturação. Para isso, vamos usar a expressão e os coeficientes que a questão nos deu. Então, a fórmula para pressão de saturação fica:
Passo 2
Vamos começar determinando a pressão de saturação para cada componente.
Para a acetona fica assim:
Para o metanol, podemos fazer o mesmo:
Passo 3
Agora que já determinamos as pressões de saturação, podemos determinar nossa pressão total através da pressão parcial e da composição molar dos dois componentes da nossa mistura.
Substituindo:
Então, a pressão que obtemos é .
Eba, finalizamos a questão. 😊 😊
Resposta
Exercício Resolvido #4
Adaptado de Lista Operações Unitárias II - UFRJ
Calcule o coeficiente de atividade dos dois componentes através da Equação de Van Laar de uma mistura de 0,4 de tolueno (1) e 0,6 de isobutanol (2) .
Considere e .
Passo 1
Para a equação de Van Laar, nós vamos utilizar:
Os coeficientes e foram os coeficientes informados na questão ( e ) e as frações molares também são conhecidas (e ).
Tudo que precisamos, então, é substituir os dados que foram dados e achar o que foi pedido 😊
Passo 2
Substituindo:
Então:
Repara que esses números são bem próximos de um, indicando comportamento próximo ao ideal 😊
Resposta
Exercício Resolvido #5
Adaptado de Lista Operações Unitárias II - UFRJ
Determine o valor da constante de equilíbrio líquido-vapor de uma mistura de 0,4 de tolueno (1) e 0,6 de isobutanol (2) a partir da equação:
Para a pressão de vapor utilize a Equação de Antoine. Para , utilize a equação de Van Laar com e .
Obs: Determine a constante de equilíbrio para os dois componentes e considere pressão igual a e temperatura de
Passo 1
Precisamos determinar a constante de equilíbrio . Para isso, temos que determinar tanto as pressões de vapor por Antoine, quanto o pela equação de Van Laar. Para a equação de Van Laar, nós vamos utilizar:
Com e para as constante e e para as frações molares. Substituindo, temos que:
Então:
Passo 2
Para a pressão de vapor, vamos utilizar a Equação de Antoine e vamos pegar os dados nas tabelas que temos disponíves, ok?
Vamos pegar os dados de cada componente:
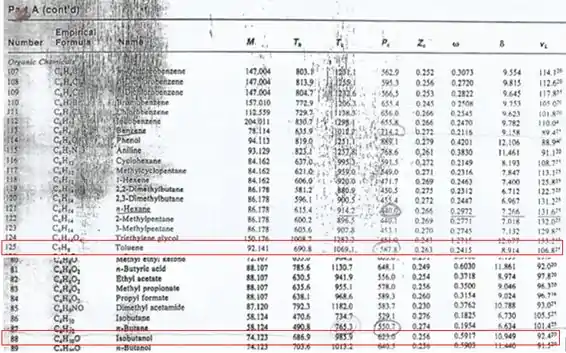
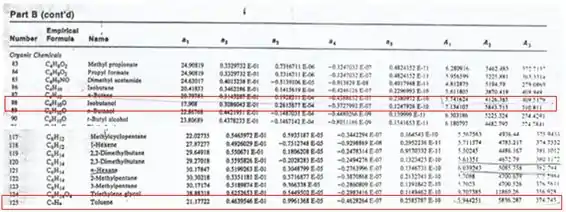
Para o tolueno, temos os seguintes dados:
Já para o isobutanol, temos os seguintes dados:
Para aplicar a Equação de Antoine, também é necessário jogar as temperaturas para Fahrenheit. Então, bora fazer essa conversão:
Então, vamos substituir a nossa temperatura de .
Passo 3
Agora, vamos substituir todos os dados nas fórmulas para encontrar a pressão de saturação de cada componente.
Para o tolueno:
Para o isobutanol:
Portanto:
Passo 4
Agora, precisamos substituir tudo que já temos na fórmula do :
Para o tolueno:
Para o isobutanol: