Regra das Fases, Diagrama e Balanço Material
Produzido por Marcelo AlvesTeoria
Regra das Fases
Vamos supor que temos um sistema líquido e vapor, constituído por 2 componentes.

Como podemos definir quais propriedades desse sistema precisamos especificar para que ele esteja totalmente especificado para os processos que vamos estudar?
Para responder essa pergunta, a primeira coisa que vamos precisar, antes de estudar os processos (Flash , Destilação e etc) é conhecer a Regra das Fases.
A Regra das Fases relaciona o grau de liberdade () de um sistema com o número de fases () e o número de componentes () presentes. E, com o grau de liberdade, a gente descobre quantas informações precisamos especificar para realizar as contas.
Olha aí a Regra das Fases:
Então, bora aplicar essa fórmula ao sistema do nosso exemplo. Temos 2 componentes e 2 fases (líquido e vapor). Logo, o grau de liberdade desse sistema é 2.
E o que isso significa?
Bem, um sistema completamente especificado tem grau de liberdade igual a zero. Logo, pro nosso sistema ficar completamente especificado, precisamos de mais duas informações sobre ele. Se a gente conhecesse, por exemplo, temperatura e pressão de pelo menos uma das fases, nosso sistema já estaria totalmente especificado.
Diagrama de Fases de uma Substância Pura
E se resolvermos aplicar essa mesma Regra de Fases para água no seu ponto tríplice (ponto que temos os estados sólido, líquido e vapor em equilíbrio), mostrado na foto aqui embaixo.
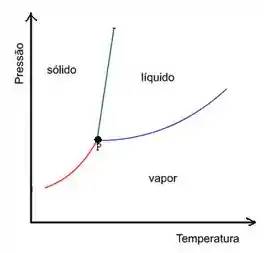
Nesse caso, nós temos só um componente, que é a água, logo . Mas, como se trata de um ponto tríplice, temos 3 fases (). Assim:
Achamos que o grau de liberdade do sistema é igual a zero. Isso indica que a água no seu ponto tríplice já está especificada, então não precisamos dar mais nenhuma informação!
Diagrama de Fases de Duas substâncias
A gente acabou de ver o diagrama de fases da água. Agora, imagina que eu quero fazer um diagrama desses, mas para uma mistura de duas substâncias... Quais seriam os eixos? Para um sistema desse tipo, podemos variar a temperatura, a pressão e a composição.
Como queremos um diagrama em duas dimensões e podemos variar três coisas, vamos precisar fixar uma delas, que, no caso, poderá ser ou a temperatura ou a pressão. O mais comum é fixar a pressão e variar a temperatura, tipo nesse exemplo do diagrama entre benzeno e tolueno.
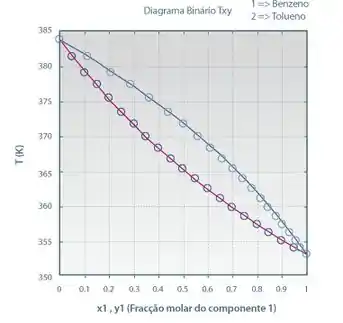
A pressão não aparece no gráfico porque ela tá fixa! Já composição e temperatura estão variando (no eixo horizontal e vertical, respectivamente).
Esse diagrama vai acompanhar a gente em muitos processos de separação, então é muito importante entender ele direitinho. Repara que estamos falando de uma mistura de benzeno (1) e tolueno (2).
E observe também que o eixo horizontal está com a composição do benzeno variando de 0 a 1 da esquerda para direita. Isso, geralmente, segue uma regrinha: a fração molar do mais volátil , que nesse caso é o benzeno, sempre varia nesse sentido, aumentando para a direita. Já a do menos volátil, que é o tolueno, varia no outro sentido. Lembrando que a fração molar dos componentes sempre soma um.
Outra observação que vai facilitar a sua vida na hora de fazer as prova é: se na direita a fração molar de benzeno é um, isso significa que temos benzeno puro. Então, aquela temperatura que está marcando ali é a temperatura de ebulição do benzeno. Da mesma forma, na esquerda, temos a temperatura de ebulição do tolueno, porque a fração molar de benzeno é 0, logo, temos tolueno puro.
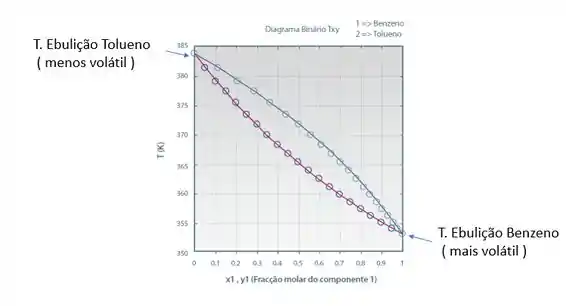
E isso faz muito sentido, pois a temperatura de ebulição do mais volátil (benzeno), de fato está menor que a temperatura do menos volátil (tolueno).
E como a gente interpreta esse diagrama? Em baixas temperaturas, vamos ter apenas fase líquida, quando chegamos em temperaturas altas, temos a fase vapor! E, no meio, entre as duas curvas, temos as duas fases coexistindo.
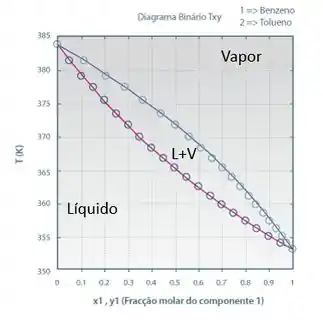
Lembrando que esse esquema que estamos mostrando só é válido para componentes a pressão constante, beleza? Aí, vamos supor que te falaram que um sistema com 0,8 de fração molar de benzeno foi submetido ao aquecimento (355 K até 370 K), a pressão constante. Vamos avaliar o diagrama para entender as informações que ele dá?
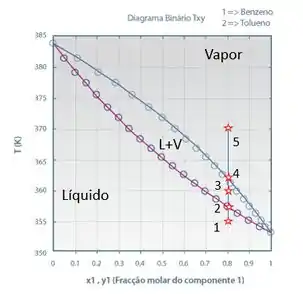
No início do processo de aquecimento, estamos no ponto 1 (. Repara que ele está na região de líquido, então a mistura é totalmente líquida, beleza?
Ao aquecermos um pouco (até o ponto 2), chegamos em um ponto super especial em que temos uma grande massa de líquido em equilíbrio com a primeira bolha de vapor. Esse ponto é chamado de Ponto de Bolha.
Se seguirmos aquecendo, chegamos ao ponto 3. Nesse ponto temos tanto fases líquida, quanto vapor. Então, nesse ponto conseguimos conhecer a composição dessas duas fases. É só traçar uma horizontal na temperatura do Ponto 3 e ler a composição nas duas curvas (tanto a do líquido, quanto a do vapor).
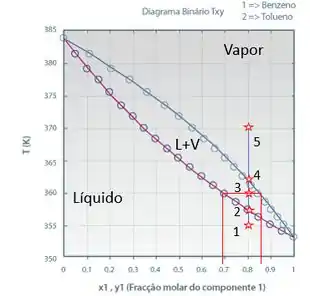
No ponto 3 o nosso vapor é constituído por cerca de 86% de benzeno, enquanto a fase líquida é composta por cercaa de 69% de benzeno.
No ponto 4 temos uma grande massa de vapor em equilíbrio com a última gotinha de líquido, então chamamos ele de Ponto de Orvalho.
E, por fim, no Ponto 5 já aquecemos tanto que só temos vapor!
Bora ver como podemos usar tudo isso para fazer contas?
Balanço Material a partir do Diagrama de Fases
Vamos supor que conhecemos o número de mols iniciais () de uma mistura e queremos saber quantos mols estão na fase vapor (e quantos mols estão na fase líquida (. Para isso, podemos realizar um balanço no próprio gráfico! Lembrando que é a fração molar global na carga (), é fração molar na fase vapor () e , na fase líquida ().
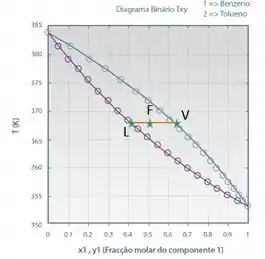
Fazendo um balanço de massa, obtemos o seguinte:
E sabemos que o número de mols total é igual ao somatório da fase líquida e vapor, então:
E aí, se reorganizarmos obtemos o seguinte:
Só que repara que o numerador ( e o denominador ( são as distâncias representadas no gráfico na retinha que traçamos entre os pontos , e , respectivamente.
Bora exercitar?