Implemente uma função que calcule as raízes de uma equação do segundo grau do tipo
Lembrando que:
Onde:
A variável têm que ser diferente de zero.
- Se não existe raiz.
- Se existe uma raiz real.
- Se existe duas raízes reais.
A função deve obedecer ao seguinte protótipo:
Essa função deve retornar à quantidade de raízes reais e da equação, e os valores das raízes devem ser armazenados nas variáveis referenciadas por e .
Passo 1
Vamos lá pessoal! Essa é uma questão de função com passagem por referência.
A questão pede pra gente criar uma função que calcula uma equação de segundo grau. Mas tem um detalhe, uma equação de segundo grau pode ter até dois resultados, porém uma função do C++ retorna apenas um único valor. Então, como podemos retornar dois valores?
É aí que entra a passagem por referência! Ao invés de retornar as raízes da equação, nós vamos passar as variáveis e como argumentos da função através de passagem por referência. Dessa forma, quando a gente alterar o conteúdo de e dentro da função, essa alteração será automaticamente aplicada nas variáveis fora da função!
Ou seja, usar passagem por referência possibilita que uma função do C++ “retorne” mais de um valor.
Com tudo isso entendido, vamos começar o nosso código. Vamos escrever o cabeçalho do código incluindo a biblioteca para facilitar nossas contas.

Passo 2
Começaremos a função.
A questão já da pra gente a assinatura da questão:
Vamos entender. Primeiro de tudo, essa é uma função do tipo ou seja, que retorna um valor inteiro. O retorna dessa função é a quantidade de raízes existentes na equação, que pode ser zero, uma ou duas raízes.
Agora vamos olhar os parâmetros. Primeiro, os coeficientes da função de segundo grau e serão recebidos através de passagem por valor com tipo .
Logo em seguida, usando passagem por referência, serão recebidos e . Essas variáveis irão armazenar os resultados da equação de segundo grau. Como elas foram passadas por referência, todas as alterações que fizermos dentro da função será refletida fora da função também.
Então vamos iniciar a nossa função:
![]()
O primeiro cálculo que temos de fazer é o do delta da equação:
![]()
Show de bola. Agora existem três possibilidades de resposta:
- Não há resposta! Isso ocorre quando ou quando
- Existe uma única resposta. Ocorre quando
- Existe duas respostas. Que ocorre quando
Então vamos desenvolver uma estrutura para considerar os três casos
Passo 3
Beleza, vamos continuar desenvolvendo a função.
A primeira situação acontece quando não existe resposta esses são os casos quando delta é menor que zero ou quando o coeficiente é igual a zero.
![]()
Na biblioteca temos a palavra-chave que significa “não é um número” (not a number). A gente usa essa palavra-chave em situações em que a resposta não pode ser calculada. Ou seja, a gente não pode calcular os valores os valores de e , então eles serão definidos como .
Além disso, o número de raízes é zero! Então vamos retornar .

O segundo caso ocorre quando . Nesse caso, as duas raízes serão iguais, então calculamos apenas uma vez, e igualamos um resultado com o outro. E como temos apenas uma única raiz, retornamos

A última situação ocorre quando . Então a gente calcula as duas raízes e retorna :

Passo 4
Agora a gente precisa testar a nossa função. Pra isso precisamos de uma
![]()
Primeira vamos declarar as duas variáveis e do tipo que vão armazenar os resultados da equação.
![]()
E também vamos precisar de uma variável inteira que armazene a quantidade de raízes existentes na equação:
![]()
Pronto! Agora é só fazer vários testes, com várias combinações diferentes de parâmetros.
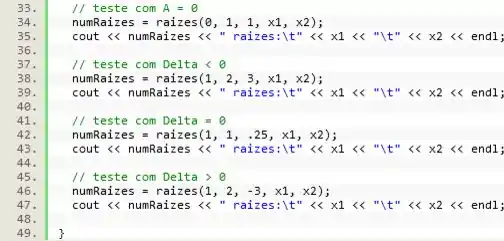
Rodando o código com todos esses testes vamos ter o seguinte resultado:
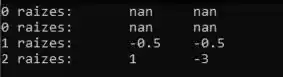
E pronto! Questão feita!
Resposta
