Rede Neural é um famoso modelo de Machine Learning, que consiste em utilizar diversos neurônios artificiais para efetuar previsões. De forma muito simplificada, um neurônio artificial efetua uma soma de todas suas entradas, e o resultado dessa soma é aplicado em uma Função de Ativação. As funções de ativação podem ser de vários tipos, mas duas muito famosas são a ReLU e a Sigmoide.
Considere um neurônio que receba entradas, faça uma função que receba como parâmetro as duas entradas e uma função de ativação, e como retorno dê o resultado do neurônio.
Para construir as funções de ativação utilize as expressões:
Para fins de simulação utilize os seguintes valores: e
Passo 1
Eita olha o tamanho do textão dessa questão. Parece até a prova do ENEM. Mas ta tranquilo, vem comigo que eu te mostro como fazer.
O que a questão está pedindo de fato é que a gente faça três funções. Uma função deve efetuar o cálculo da ReLU, a segunda função efetua o cálculo da Sigmoide.
Já a terceira função simula o neurônio da rede, e ela possui três parâmetros, os valores e e o terceiro parâmetro deve ser o ponteiro para uma função.
E depois que a gente construir as funções, dentro da nossa a gente vai executar as funções.
Mas antes de fazer tudo isso, vamos começar com o cabeçalho do programa

Passo 2
Certo, então primeiro vamos desenvolver as funções
Vamos começar desenvolvendo a função ReLU. Essa é uma função composta, se o valor de for menor que zero, então o resultado é . Se o valor de for maior que zero, então o resultado é igual ao próprio valor de . A gente pode traduzir isso em uma condição da seguinte forma:
Em termos de código, essa função deve ser do tipo e receber uma única entrada do tipo . O código fica da seguinte forma:

Passo 3
Agora vamos desenvolver a função sigmoide. Vamos criar uma função que execute a seguinte expressão:
Pra desenvolver essa expressão vamos criar uma função do tipo que recebe um único parâmetro do tipo também. O código é:

Passo 4
O próximo passo é desenvolver a função . Primeiro de tudo precisamos determinar os parâmetros. Vamos receber dois valores do tipo e . A função de ativação também será recebida como um parâmetro, então o terceiro parâmetro da função é um ponteiro para a função de ativação
![]()
O corpo da função neurônio vai efetuar uma soma dos parâmetros e . Então criamos uma variável chamada que armazena o resultado de .
![]()
Em seguida precisamos aplicar o resultado da soma na função de ativação. Por isso, agora você tem que lembrar que o ponteiro de uma função é um apelido para função original. Por isso podemos fazer a expressão:
E assim conseguimos executar a função apontada pelo ponteiro . Então vamos armazenar o resultado da numa variável chamada
![]()
E pra concluir a função vamos retornar o valor guardado em
![]()
Passo 5
Com as nossas funções prontas podemos construir a nossa
A questão nos diz para utilizar os seguintes valores e como entrada do nosso neurônio, então vamos declará-los no início da
![]()
A questão pede que a gente execute o neurônio duas vezes, da primeira vez com a função relu, e da segunda vez com a função sigmoide. Então vamos declarar duas variáveis para guardar estes resultados.
![]()
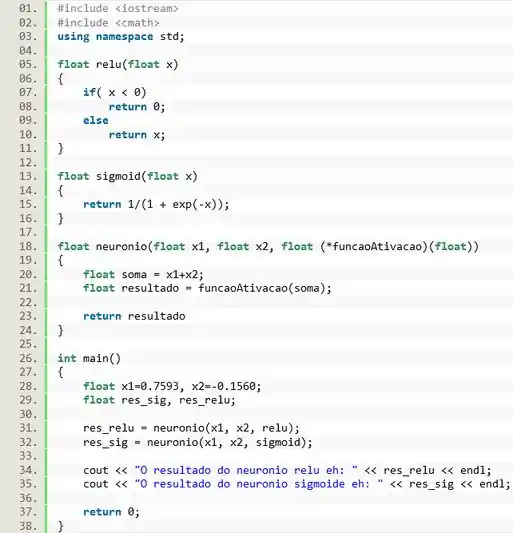
O próximo passo é executar os neurônios. Vamos executar a função passando como parâmetro os valores e e a função , e guardamos o resultado na variável . Em seguida fazemos o mesmo, mas passando a função como parâmetro e guardando o resultado na variável .

E pra finalizar a questão, é só a gente utilizar a função para mostrar os resultados

Executando o programa, teremos o seguinte resultado:
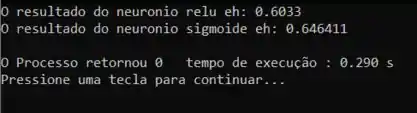
Resposta