10-16. Está sendo investigada a temperatura em que ocorre uma defle

xào, devido à carga. em dois tipos diferentes de tubo plástico. Duas

amostras aleatórias de 15 tubos são testadas e as temperaturas (em '℉)

observadas em que ocorre a dellexão são reportadas a seguir:

a) Construa diagramas de caixa e gráficos de probabilidade normal para

as duas amostras. Esses gráficos confirmam as suposições de nor-

malidale e variâncias iguais? Escreva uma interpretação prática para

Csses gráficos.

b) O- dados confirmam a afirmação de que a temperatura em que ocorre

a deflexáo, devido à carga, do tubo tipo 1 excede àquela do tipo 2?

Para concluir algo, use a - 0,05. Caleule o valor P.

c) Se a temperatura média em que ocorre a deflexão do tubo tipo |

exeeder aquela do tubo tipo 2 por 5°F. é importante detectar essa

diferença com probabilidade de no minimo 0.90. A escolha de n,=

n, = 15 é adequada? Use a - 0.05.

Letra a:

Gráfico da probabilidade normal:

Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.

Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .

A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.

Tipo 1:

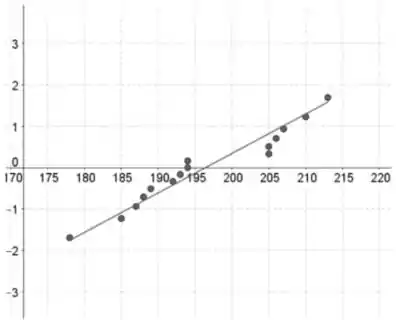
Tipo 2:

Diagrama de caixa:

Os bigodes do diagrama de caixa estão nos valores mínimo e máximo. A caixa começa no quartil inferior e termina no quartil superior e tem uma linha vertical na mediana.

O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.

A suposição de normalidade parece válida, porque os padrões nos gráficos de probabilidade normal são aproximadamente lineares e não continham nenhuma curvatura forte.

A suposição de médias iguais parece válida, porque os diagramas de caixa têm aproximadamente a mesma largura.

Letra b:

Determine as hipóteses:

Determine o desvio padrão agrupado:

Determine a estatística de teste:

Determine o valor P correspondente da tabela de distribuição T-Student no apêndice com :

Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:

Não há evidências suficientes para apoiar a alegação de que as médias da população são diferentes.

Letra c:

é o complemento da potência, assim, 1 diminuiu pela potência.

Fórmula do tamanho da amostra é:

:é a hipótese nula

é a hipótese alternativa .

Determine usando a tabela III (procure na tabela. O valor z é então o valor z com o sinal oposto):

Determine usando a tabela III (procure na tabela. O valor z é então o valor z com o sinal oposto):

Preencha os valores conhecidos na fórmula e avalie (arredondar para cima!):

Uma vez que este tamanho de amostra é muito maior do que os tamanhos de amostra usados ​​de 15, o tamanho da amostra de não é adequado.