10.17. Na fabricacão de semicondutores. o ataque quimico por via úmida

e treqüentemente usado para remover silicone da parte posterior das

atilhas antes da metalização. A taxa de ataque é uma caracteristica

mportante nesse processo e é sabido que ela segue uma distribuição

ormal. Duas soluções diferentes para atkque quimico têm silo compa-

adas. usando duas amostras aleatórias de 10 pastilhas para cada solu-

As taxas observaklas de ataque (10 'mils/min) são dadas a seguir:

1. Construa gráficos de probabilidade normal para as duas amostras.

Esses gráficos confirmam as suposições de normalidade e variânci.

as iguais? Escreva uma inlerpretação pratica para esses gráficos.

2. s dados confirmam a afirmação de que a taxa média de ataque é a

mesma para ambas as soluções? Para concluir algo, use

considere que ambas :as populações têm variâncias iguais. Calcule o

valor P.

3. Encontre um intervalo de confianca le 95% para a diferenca de ta

vas médias de ataque químico.

Letra a:

Gráfico da probabilidade normal:

Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.

Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .

A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.

Solução 1:

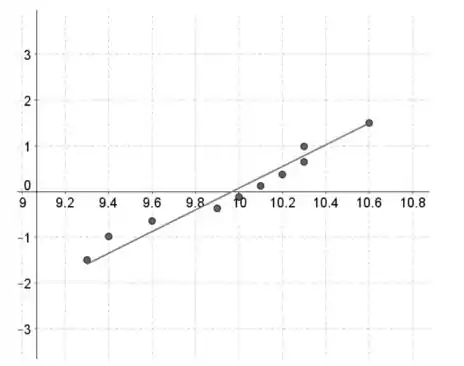
Solução 2:

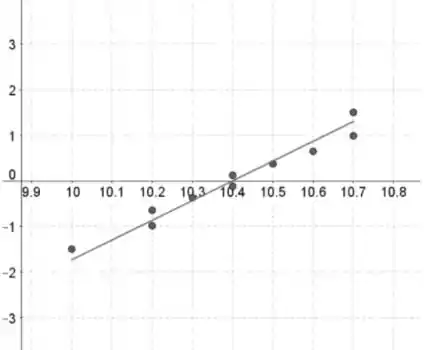
O sintoma de normalidade parece ser válido, já que os padrões nos gráficos de probabilidade normal são aproximadamente lineares e não contêm nenhuma curvatura forte.

A associação de variâncias iguais parece ser válida, porque a razão dos desvios padrão (maior para menor) é menor que 2.

Letra b:

Determine as hipóteses:

Determine o desvio padrão agrupado:

Determine a estatística de teste:

Determine o valor P correspondente da tabela de distribuição T-Student no apêndice com :

Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:

Há evidências suficientes para apoiar a alegação de que os meios da população são escassos.

Letra c:

Determine correspondente da tabela de distribuição T-Student que é dada na coluna e na linha com:

Os pontos finais do intervalo de confiança para são:

Estamos confiantes de que a taxa de corrosão média para a solução 1 está entre mils/minuto e mils/minuto menor do que a taxa de corrosão média para a solução 2.