Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 76
10-76. Um experimento toi conduzido para comparar a capacilade de
enchinenio de um cquipamento de eimpacolamento em luas diferenles
vinicolas. Dcz garrafas de Pinot Noir, provenientes da Vinicola Ridge-
crest. foram seiecionadas aleatoriamente e medidas. juntamente com 10
garrafas «de Pinot Noir, provenientes da Vinicola Valley View. Os da-
dos fos volumes de enchimento estào em mililitrosi são apresentados
a seguir:
a) Quais são as suposiçães necessárias para claborar um procedimeato
de teste de hipoteses para a igualdade das medias desses dados?
Verifique essas suposicoes.
b)Faca o procedimento apropriado de leste de hipóteses para determi-
nar se os dados confirmam a afirmacão de que ambas as vinicolas
encherão garralas com o mesmo volume medio.
c) Suponha que a diferenca verdadeira no volume medio de enchimen
lo seja igual a 2 onças luidas. O tamanho de amostra igual a 10 para
cada vinicola fomeceu uma boa capcidade de sleleccão quando
a - 0.05? Eixplique sua resposta.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividido por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Exigimos que as distribuições sejam distribuídas aproximadamente normalmente.
Gráfico da probabilidade normal:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
Passo 3
Amostra 1:
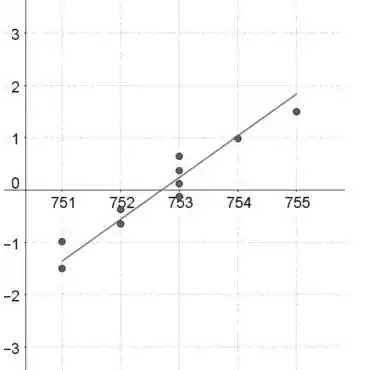
Amostra 2:
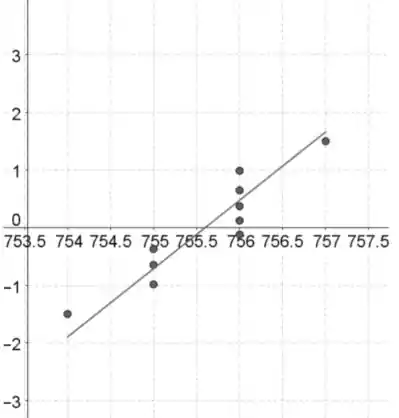
A suposição normal parece ser satisfeita, porque o padrão em ambos os gráficos de probabilidade normal é aproximadamente linear, o que indica que as distribuições são aproximadamente normalmente distribuídas.
Passo 4
Letra b:
Determine a estatística de teste:
Determine os graus de liberdade (arredondados para o número inteiro mais próximo):
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t no na linha
Se o valor P for menor ou igual ao nível de significância, a hipótese nula é rejeitada:
Há evidências suficientes para rejeitar a alegação de que ambas as vinícolas encherão garrafas com o mesmo volume médio.
Passo 5
Letra c:
Dado:
Fórmula do tamanho da amostra:
é a hipótese nula em
é a hipótese alternativa
Determine usando a tabela lll (procure 0.025 na tabela. O valor z é então o valor z encontrado com sinal oposto):
Preencha os valores conhecidos na fórmula e avalie (arredonda para cima!):
Os tamanhos das amostras de 10 são adequadas, porque são maiores do que o tamanho mínimo de amostra exigido de 3.
Resposta
- Premissas satisfeitas
- Há evidências suficientes para apoiar a alegação de que os volumes médios são diferentes
- Sim