Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 29
10-29. Considere o experimento da resistencia ao cisalhamento descri-
to no Exemplo 10-9.
a) Construa, usando os dois métodos. o intervalo de confianca de 9596
para a diferença na resisténcia média ao cisalhamento. O resultado
que vocé obteve é consistente com o que voce encontrou no Exem
plo 10-92 Exphque por qué.
b) Cada uma das duas resistencias cisalhantes individuais tem de ser
normalmente distribuida para o teste t emparelhado ser apropriado?
Ou é somente a diferenca nas resistencias cisalhantes que tem de ser
normal? Use um grático de probabilidade normal para investigar a
supxsição de normalidade.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
diferença das médias
diferença de desvio padrão
Tamanho da amostra
Nível de confiança
Letra a:
Determine usando a tabela de distribuição T-Student, que é dada na coluna com e na linha com:
Os pontos finais do intervalo de confiança são então:
Passo 2
Letra b:
As diferenças devem ser distribuídas aproximadamente normalmente, porque o teste t é aplicado às diferenças e não às distribuições individuais.
O gráfico de probabilidade normal será assim:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
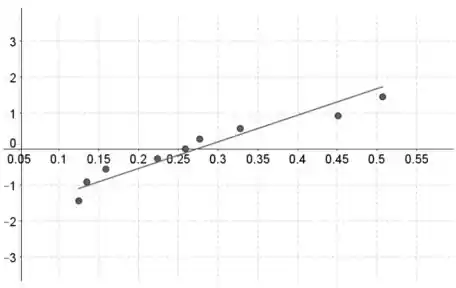
A suposição normal parece satisfeita, porque o padrão na probabilidade normal é aproximadamente linear e não contém nenhuma curvatura forte.
Resposta
- Diferença nas resistências ao cisalhamento
A suposição normal é satisfeita.