Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 7
11-7. Um artigo no Tappi Journal (Março de 1986) apresentou dados
sobre a concentraçân do licor verde de Na,S e da producão de uma
máquina de papel. Os dados (lidos a partir de um gráfico) sáo mostra-
dos na seguinte tabela.
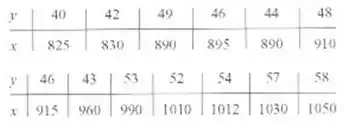
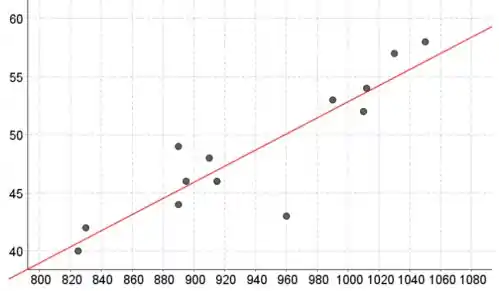
a) Ajuste um modelo de regressão lincar simples, relacionando a con-
centração do licor verde de Na.S. y. com a produção, A. Desenhe um
diagrama de dispersáo dos dados e o modelo resultanle do ajuste pelo
métoxlo dos minimos quadrados.
b) Encontre o valor ajustado v. correspondente ax 910.co residuo
assuciado.
c) Encontre a concentração média do licor verde de Na,S quando a taxa
de produção for de 950 toneladas por dia.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Letra a:
As estimativas de mínimos quadrados da interceptação e inclinação são:
A linha de regressão de mínimos quadrados torna-se então:
Determine a soma dos erros quadrados:
é então estimado pela soma dos erros quadráticos divididos pelo tamanho da amostra diminuída por 2:
Passo 2
Letra b:
Substitua x na linha de regressão de mínimos quadrados por 910 e avalie:
O resíduo é o valor real diminuído pelo valor previsto:
Passo 3
Substitua x na linha de regressão de mínimos quadrados por 950 e avalie: