Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 25
Um estudo pretende avaliar o efeito da obesidade na pressão sanguínea. Para tanto, foram avaliados os pesos para 6 indivíduos e construída a variável representando a razão entre os pesos real e ideal. Estudos indicam que um modelo de regressão linear simples é adequado para essa situação. Os dados obtidos foram:
- Construa a variável auxiliar
- Ajuste a reta
- Qual a sua interpretação para na reta obtida em (b) ?
- Qual a pressão sistólica esperada para indivíduos com razão peso real/peso ideal igual a 1,25??
Passo 1
Eu indo matar mais uma questão de estatística:
É de regressão linear:
Vamos lá então; a questão pede que realizemos o teste para ver se a razão entre o peso real e o ideal estabelece uma relação linear com a pressão sistólica; tendo:
E
Queremos saber se essa reta é verdade:
Onde e são estimadores para os coeficientes linear e angular respectivamente.
Perceba que tudo o que queremos é saber se esse realmente é zero ou não, se ele for diferente de zero então existe uma relação linear; em outras palavras:
Como fazeremos isso mesmo??? Utilizando a aproximação pela distribuição :
Os quadrados médios são calculados a partir das somas dos quadrado, veremos daqui a pouquinho, juro. Já esse é o número de variáveis, portanto e é o tamanho das amostras.
Bom, o enunciado definiu da seguinte forma:
E os estimadores podem ser obtidos assim:
E
Passo 2
Então, vamos começar encontrando essa galera aí:
Agora, tem um detalhe muitíssimo importante!! Percebeu que a gente não vai trabalhar com para realizar a regressão, mas sim com . Da uma olhada na tabela:
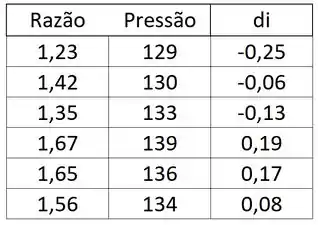
Lembrando que .
Com isso, podemos tirar alguns dados que vamos precisar para estimar a reta e realizar a regressão:
e
E portanto:
Portanto, temos a seguinte estimação para a reta:
Se você se lembrar, devemos montar uma tabela mais ou menos assim:
Eu sei que assusta um bocado, mas não é nenhum bixo de sete cabeças, juro!
Da uma olhada com carinho na tabela, vamos precisar de todos os ; encontrando eles a partir da reta que estimamos. Então teremos que fazer o seguinte:
Até..
Sacou a parada? Juntei tudo numa tabelinha, olha só:
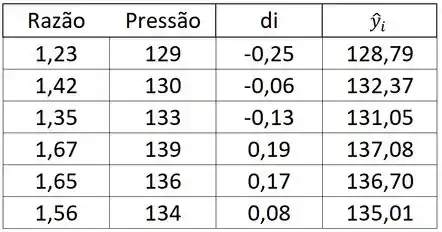
Ta junto comigo?? Seguimos...
E
Passo 3
Tamo quase lá...
Em posse das Soma de Quadrados(SQ), podemos encontrar os Quadrados médios(QM); bate o olho la na tabela que estamos usando como modelo para fazer a nossa regressão:
E
Em posse dos quadrados médios, podemos calcular o :
Finalmente completamos nossa tabelinha:
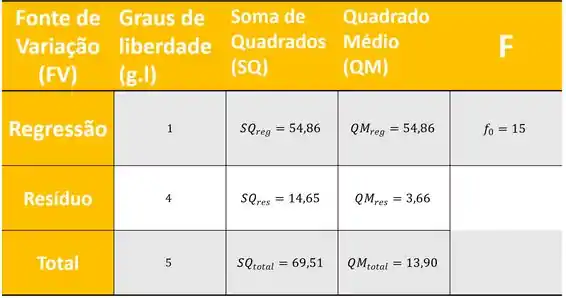
Beleza, cabou então?? Ainda não pequeno gafanhoto... Precisamos analisar aquele para tomar uma decisão.
Lembra que fazemos isso construindo uma região crítica?? Então adotando :
Portanto, só precisamos ir na tabela de distribuição a 5%, e buscar na coluna de grau de liberdade, e na linha de graus de liberdade:
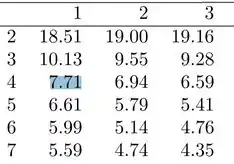
Chegamos na seguinte região crítica:
Portanto, como pertence à região crítica, devemos rejeitar a hipótese nula que diz que .
Isso da evidências de que realmente há uma relação linear entre a pressão sistólica e a razão entre os pesos.
Resposta
Portanto, concluímos que a pressão sistólica estabelece uma relação linear com a razão entre os pesos real e ideal.
(c) o na reta, representa o valor esperado de pressão sistólica quando a razão entre os pesos for ; perceba:
Como , e então
quando .
(d)O exercício pede ainda para encontrarmos a pressão sistólica quando a razão entre os pesos for 1,25. Bem sussa: