11-86. Dois diferentes métodos podem ser usados para medir a tem-

peratura da solução cm uma célula de Ilall usada na fusão de alumí-

nio: uin lerinopar implantado na célula e uma mediçào indireta pro-

duzida em um dispositivo de IV. O método indireto é preferivel devi

do à desiruição dos termopares pela solução. Considere as 10 medidas

seguintes:

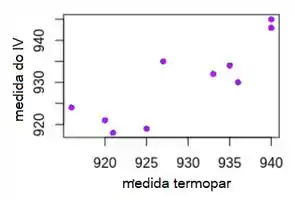
a) Construa um diagrama de dispersão para esses dados, sendo x

medida do termopar e y = medida do IV.

b) Ajuste um modelo de regressào linear simpies a esses dados.

c) Teste a significância da regressão e calcule R'. Que conclusòes vocé

pode tirar?

d) Há evidéncia para sustentar a afirmação de que ambos os dispositi

vus produzem medidas cquivalentes de temperatura? Formule e tes-

te uma hipólese aprupriada para sustentar essa afirmação.

e) Analise os resíduos e comente a adequação do modelo.

Letra b:

Primeiro, vamos calcular as quantidades importantes (nota que .

Agora estamos prontos para determinar os coeficientes do modelo:

Portanto, o melhor ajuste linear para os dados é:

Letra c:

Precisamos testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema.

Primeiro, avalie a regressão e a soma dos quadrados dos erros:

para calcular o valor da estatística F:

Rejeitamos então primeiro, vamos determinar:

e concluímos que rejeitamos Portanto, o modelo é significativo. Calcule o coeficiente de determinação:

Nomeadamente, cerca de 71% da variabilidade é explicada pelo modelo, que é substancial.

Letra d:

O termo de interceptação no modelo não é significativo , ou seja, não há evidências para apoiar, (a estimativa é grande, mas o erro padrão é enorme, verifique)

Portanto, podemos dizer que o modelo é:

com a estimativa da inclinação sendo

É razoável testar a seguinte hipótese:

com relação à alternativa bilateral. Vamos fazer isso.

A estatística de teste é a seguinte:

Calcule o valor t, para este teste (alternativa bilateral, )

portanto, por causa de , não podemos rejeitar a hipótese nula de .

Finalmente, podemos realmente dizer que há evidências para apoiar o modelo:

ou seja, há evidências para apoiar que ambos os dispositivos produzem medições de temperatura equivalentes.

Letra e:

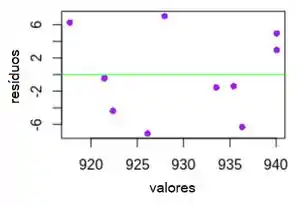
Plote os resíduos do modelo em relação aos valores ajustados para a resposta e examine o gráfico.

Concluímos que a variância não é a mesma em todo o intervalo dos dados, porque os resíduos são muito menores para os maiores valores ajustados.

Portanto, o modelo não é totalmente adequado.