Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 76
11-76. A pressao do vapor d'água em vánias temperaturas é dada a seguir:
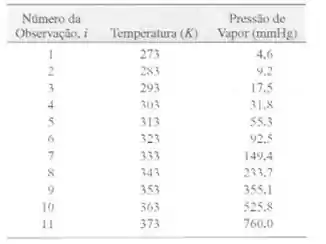
a) Desenhe um diagrama de dispersão desses dados. Que tipo de rela-
cão parece apropriada relacionando y com .r?
b) Ajusle um modelo de regressao linear a esses dados.
c) Teste a significância da regressão usando a =0.05. Que conclusoes
voce pode tirar?
d) Faça um gráfico dos residuos do modelo de regressão versus y. O
que vocé conelui acerea da adequacao do modelo!
e) A relação de Clausius-Clapeyron estabelece que IniP.) x-y,em
que P.é a pressão do vapor d'água. Repita os itens (a)-(d).usando
uma transformação apropriada.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Letra a:
Denotemos a variável de temperatura em Kelvins com a letra x, e a variável aleatória de pressão de vapor em mmHg com a letra y. Então, depois do processamento dos dados fornecidos na tabela, chegamos ao seguinte gráfico de dispersão dos dados:
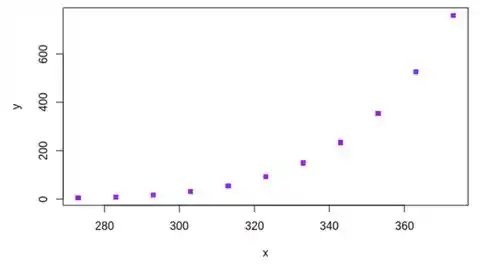
É evidente a partir deste gráfico que a variável y é exponencialmente dependente da variável x. Ou seja, a pressão de vapor aumenta exponencialmente com o aumento da temperatura.
Passo 2
Letra b:
Agora ajustamos o modelo linear aos dados. Primeiro, vamos calcular as quantidades importantes (nota :
Agora estamos prontos para determinar os coeficientes do modelo:
Portanto, o melhor ajuste linear para os dados é:
Passo 3
Letra c:
Precisamos testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema. Primeiro, vamos avaliar a regressão e a soma dos quadrados dos erros:
para calcular o valor da estatística F:
Rejeitamos então primeiro determine:
e então rejeitamos
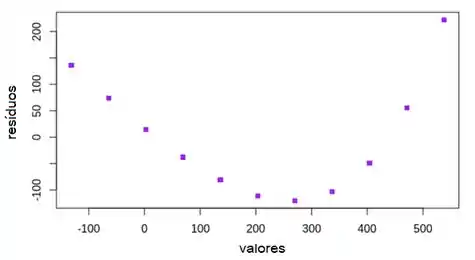
Passo 4
Letra d:
Na foto acima, os resíduos são representados graficamente em relação aos valores ajustados do modelo. Este gráfico sugere que o modelo não é adequado. Um forte padrão curvo é observado, e os resíduos definitivamente não variam aleatoriamente com respeito a qualquer eixo.
Passo 5
Letra e:
Aplique as transformações fornecidas para obter novas variáveis da seguinte forma:
Agora repita a análise em ordem.
Primeiro, vamos calcular as quantidades importantes (nota ):
Agora estamos prontos para determinar os coeficientes do modelo:
Portanto, o melhor ajuste linear para os dados é:
Passo 6
Agora precisamos testar a significância da regressão. Neste exercício, optaremos pela abordagem de análise de variância para este problema. Primeiro, vamos avaliar a regressão e a soma dos quadrados dos erros:
para calcular o valor da estatística F:
Obviamente, rejeitamos
Resposta
- Ver resolução