Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 12.Exercícios - Ex. 51
12-51. Considere ns dados de consumo de gasolina do Exercicio 12-5.
a) Quc proporção da variahilidadc total é explicada por esse modelo?
b) Consinua um gráfico de probabilklade normal dos resíduos e comente
a suposição de normmalidade.
c) Plote os residuos contra ve contra cada regressor. Discuta esses grá-
fieos dos residuos.
d)Calcule a distância Cook para as observações nesse conjunto de
dklos. Existe aleuma observacão iniluente?
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Neste exercício, você deve usar os dados fornecidos no exercício 12.5.
Letra a:
Para calcular o coeficiente de determinação-precisam ser obtidos. Portanto:
Finalmente,
Concluímos que cerca de 89.3% da variabilidade total é explicada pelo modelo.
Passo 2
Letra b:
Agora traçamos o gráfico de probabilidade normal para os resíduos (abaixo). Vemos que a suposição de normalidade é razoavelmente justificada, mas não perfeitamente.
Passo 3
Letra c:
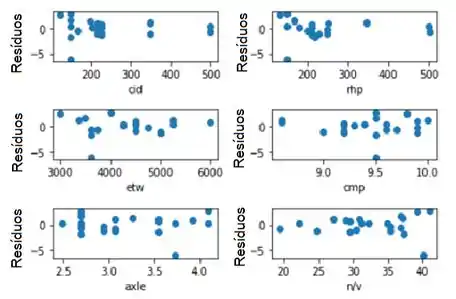
Agora traçamos os resíduos em relação a todos os regressores (Abaixo). Vemos que vários regressores se comportam de maneira diferente, mas geralmente exibem variância homogênea.
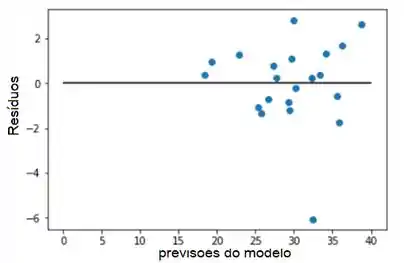
Finalmente, traçamos o gráfico residual usual de resíduos versus previsões do modelo. Concluímos que os resíduos são dispersos aleatoriamente ao longo do eixo vertical (ou seja, em torno de y= 0), que é o comportamento desejado.
Passo 4
Letra d:
Calcule a distância de Cook para todas as observações de acordo com a fórmula:
onde resíduo, e k=6 número de variáveis.
Nenhuma observação foi considerada influente.
Resposta
- Ver resolução
- Ver resolução
- Nenhuma observação foi considerada influente.