Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 13.Exercícios propostos - Ex. 9

Abaixo se encontram os dados da ANFAVEA (Assoc. Nacional dos Fabricantes de Veículos Automotores), em milhares:

Pede-se:

a) ajustar uma reta;

b) ajustar uma função exponencial;

c) calcular os coeficientes de explicação, interpretando-os;

d) construir o intervalo de confiança de f ( x ) para o ano de 1977, tanto para a linear quanto a exponencial, para α = 0,10

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão dados os itens abaixo,

Encontre:

a) ajustar uma reta;

b) ajustar uma função exponencial;

c) calcular os coeficientes de explicação, interpretando-os;

d) construir o intervalo de confiança de f ( x ) para o ano de 1977, tanto para a linear quanto a exponencial, para α = 0,10

Passo 2

Na letra (a) sabendo que,

x - = 0 y - = 2898 6 = 483

y = 3132 70 = 44,72

y = 483 + 44,74 x

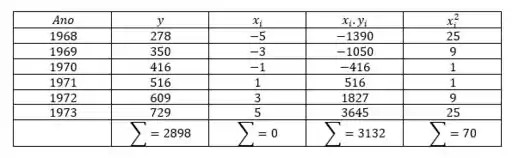
Passo 3

Na letra (b) para ajustar na função exponencial, temos

log ⁡ W = y log ⁡ A = a log ⁡ B = b → w = A . B x →     w = 458,14.1005 γ

Na letra ( c ) o coeficiente de explicação fica,

R 2 = V E V T = b 2 . s x x s y y = 98,9 %   ( r e t a )

R 2 = V E V T = b 2 . s x x s y y = 9 9,2   % ( e x p o n e n c i a l )

Na letra (d) para construir o intervalo de confiança de f ( x ) para o ano 1977, tanto para linear e exponencial, com α = 0,10 temos,

Na reta: 997,010 ≤ f x ≤ 1132.230

Na exponencial: 1590740 ≤ f x ≤ 1591040

Bem simples né? Aqui no responde aí é assim tudo fica simples que a gente nem percebe. Espero ter ajudado e até a próxima.

Resposta

a) y = 483 + 44,74 x

b) w = 458,14.1005 γ

c) R 2 = V E V T = b 2 . s x x s y y = 98,9 %   ( r e t a )

R 2 = V E V T = b 2 . s x x s y y = 99,2   % ( e x p o n e n c i a l )

d) Na reta: 997,010 ≤ f x ≤ 1132.230

Na exponencial: 1590740 ≤ f x ≤ 1591040

Exercícios de Livros Relacionados

A taxa de fluxo y ( m 2 / m i n . em um dispositivo usado para avaliar a qualidade do ar depende da queda de pressão x (polegadas de água) por meio do filtro do dispositivo. Suponha que, para x valore
O artigo "Some Field Experience in the Use of an Accelerated Method in Estimating 28-Day Strength of Concrete" (J. Amer. Concrete Institute, 1969, p. 895) experimentou regredir a resistência a tratame
Um dos fatores do desenvolvimento do "cotovelo de tenista" (tennis elbow), doença que amedronta todos os tenistas praticantes, é a vibração induzida pelo impacto da raquete e do braço no contato com a
Em relação ao Exercício 7, suponha que o desvio padrão do desvio aleatório ϵ seja 350 psi.a. Qual é a probabilidade de o valor observado de resistência aos 28 dias ultrapassar 5000 p s i , quando o va
Suponha que o custo esperado de uma operação de produção esteja relacionado com o tamanho da operação por meio da equação y 4000 10x. Seja Y uma observação sobre o custo de uma operação. Se as variáve