12-69. Um artigo na revista Journat of Pharmaccuticals Sciences i Vol.
80,1991.pp.971-977) apresenta dados sobre a solubilidade observada
(expressa em fração molar) de um soluto, a uma temperatura constanle,
e sobre os parametros de solubilidade parcial do moxdelo de Hansen.
referentes à dispersáo. ao momento dipolo e às ligaçóes de hidrogenio.
Os dados são mostrados na tabela seguinte. em que v é o logantmo ne-
gativo da solubilidade e x, é a solubilidadc parcial da dispersão, v. é a
solubilidade parcial dipolar e x, é a solubilidadc parcial da ligação de
hidrogénio.
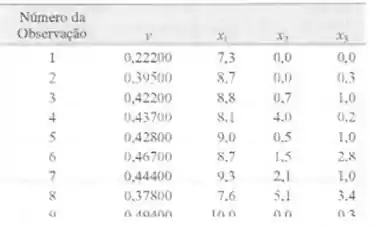
a) Ajustc o modelo
b) Teste a significância da regressão usando - 0.05.
c) Plote os residuos e comente a adequação do modelo.
d)Use o nétodo da soma extra dos quadrados para testar a contribui-
cão dos termos de segundo grau usando a = 0.05.
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Letra a:
Ajuste o modelo de regressão linear (neste caso - modelo polinomial de 2ª ordem) para obter:
Passo 2
Letra b:
A estatística de teste F deve ser calculada da seguinte maneira.
Nós sabemos que:
Vamos lembrar que:
Em seguida, calcule a partir dos dados:
Agora podemos calcular:
Portanto, a estatística F é
O valor P para o teste de significância da regressão é então obtido como
A hipótese é então rejeitada e a regressão é significativa.
Passo 3
Letra c:
Plote os resíduos do modelo versus as previsões do modelo. O gráfico sugere que o modelo é moderadamente adequado.
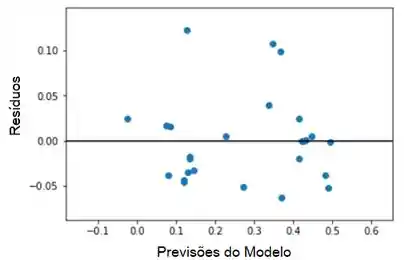
Além disso, faça o gráfico de probabilidade normal. A suposição de normalidade dos resíduos não parece completamente satisfeita
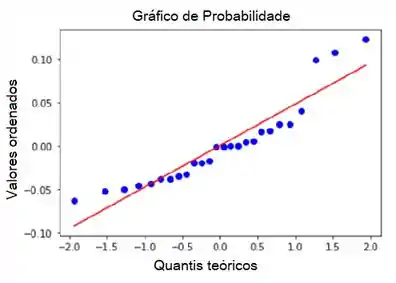
Passo 4
Letra d:
Lembre-se de como o teste F parcial é feito e o que isso significa.
Defina r=6 e
Então,
A estatística de teste F deve ser calculada da seguinte maneira.
Lembre-se que:
Então você tem que calcular (tendo em mente que esses números são obtidos a partir de modelos completamente diferentes!):
Portanto, a estatística F é
O valor P para o teste de significância da regressão é então obtido como
A hipótese
não é, portanto, rejeitada, o que significa que a contribuição da variável não é significativa para o modelo.
Resposta
- Ver resolução