Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 74
9.74. Se o desvio-padrão do diámetro do onfico exceder 0,001 milímetro, há uma probabilidade inaceitavelmente alta de que o rebite não se ajustará. Suponha que n
(a) Ha uma forte evidéncia indicando que o desvio-padrão do diâmetro do orificio excede 0,01 milimetro? Use a -,01. Estabeleça quaisquer suposiçãs necessárias acerca da distribuição em foco dos dados. Encontre o valor P para esse teste.
(b) Suponha que o desvio padrão real do diametro do orificio exceda por 50% o valor usado na hipotese. Qual é a probabilidade de que essa diferença eja detectada pelo teste descrite no item (a)?
(c) Se o é realmente tão grande quanto 0,0125 milimetro, que tamanho de amostra será necessário para detectar isso com poténcia de no mí 15 es 0,00 milímetro?
Passo 1
Oi oi gente, tudo bom com vocês?
Vamos fazer essa questão aqui de um jeito bem passo a passo pra facilitar a vida de todo mundo!Boraaa
Suponha que desejamos testar a hipótese de que a variância de uma população normal é igual a . Seja uma amostra aleatória de uma observação desta população. Para testar
vamos usar a estatística de teste:
(1)
A estatística de teste definida na Equação (1) segue a distribuição qui-quadrado com graus de liberdade, se a hipótese nula é verdadeira. Para realizar um teste de nível de significância fixo, pegaríamos uma amostra aleatória da população de interesse e calcularíamos , que é o valor da estatística de teste e a hipótese nula seria rejeitada se:
(2)
onde é o ponto percentual da distribuição qui-quadrado com graus de liberdade.
O valor P para um teste de cauda inferior seria encontrado como a área (probabilidade) na cauda inferior da distribuição do qui-quadrado à esquerda (ou abaixo) do valor calculado da estatística de teste . Para a alternativa de dois lados, encontre a área da cauda associada ao valor calculado da estatística de teste e duplique-a para obter o valor P.
Portanto, o valor P para este teste é:
Sabemos que e milímetros.
Passo 2
Letra a:
Consideramos o teste de contra .
Agora, da Equação (1) obtemos valor para a estatística de teste
Para e da Tabela IV do Apêndice, obtemos.
Então
Agora, da Equação (2), concluímos que falhamos em rejeitar .
O valor P para este teste é obtido da Equação (3).
Nós sabemos do que do Apêndice Tabela IV, temos
Então
Portanto, o valor P é
Passo 3
Letra b:
Suponha que o desvio padrão real do diâmetro do furo exceda o valor hipotético em 50%, então
Então,
Este é o parâmetro de abscissa do Gráfico VIII ). A partir deste gráfico, com e , encontramos que (Linha vermelha). Portanto, há apenas cerca de 40% de chance de que a hipótese nula seja rejeitada se o verdadeiro desvio padrão for realmente tão grande quanto .
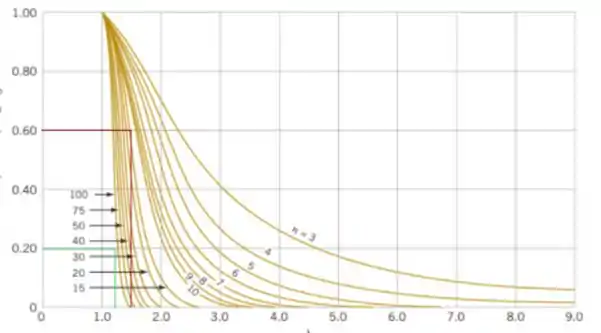
Passo 4
Letra c:
Para reduzir o erro , um tamanho de amostra maior deve ser usado. Da curva característica operacional com e
descobrimos que , aproximadamente (veja a figura anterior, linha verde). Portanto, se quisermos que o teste seja executado conforme necessário, o tamanho da amostra deve ser de pelo menos 100.
Resposta
- Falhamos em rejeitar , porque ,
- Existe apenas cerca de 40% de chance de que a hipótese nula seja rejeitada.