Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 33
Acredita-se que o empenho de estudantes universitários muda no decorrer do curso. Para investigar essa afirmação, decidiu-se estudar a relação entre o ano de curso e aprovação em disciplinas. Os pesquisadores obtiveram os registros de 186 estudantes universitários, selecionados aleatoriamente, dentre a totalidade de alunos de uma certa instituição de ensino superior. Foram consideradas 3 disciplinas básicas em cada ano. Os resultados obtidos foram resumidos e são apresentados na tabela a seguir.
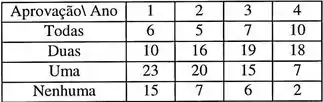
- Quantifique o grau de associação entre aprovação e ano cursado.
- Teste a hipótese de que as duas variáveis são independentes, ao nível de significância de .
- Obtenha o nível descritivo.
Passo 1
Bora matar mais uma, seguinte, aqui também vamos realizar o teste de independência para as variáveis:
E
Na letra A ele pede o grau de associação entre as duas variáveis, isso nada mais é do que encontrar:
Que representa a aproximação pela distribuição Qui-quadrado, com graus de liberdade; onde é o número de linhas e colunas.
Temos ainda, que representa os valores OBSERVADOS em CADA CÉLULA; e representa os valores ESPERADOS também para cada célula.
Ora, os valores observados nós já temos, são os valores da tabela no enunciado; top show.
Só precisamos encontrar os valores esperados, e fazemos isso da seguinte forma:
E assim por diante até:
Um bocado trabalhoso né?! Só vamo!
Passo 2
Começando essa bagaça então! Para facilitar, refiz a tabela com os valores totais:
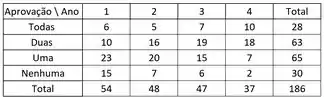
E assim por diante, até:
Aí vamos organizar todos esses valores esperados numa tabelinha:
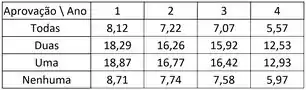
Bateu tudo aí?? Então seguimos...
Agora, finalmente podemos calcular a aproximação pela Qui-quadrado:
É justamente esse o grau de associação entre as variáveis.
Passo 3
Top! Tamo quase! Agora precisamos realizar o teste propriamente dito, temos:
E precisamos ver se aquele valor que encontramos está dentro da região crítica ou não.
Nossa região crítica será:
Como nosso , precisamos buscar na tabela de distribuição Qui-quadrado, um valor tal que:
Para tanto, basta irmos justamente na coluna que representa 5% e buscarmos a intersecção com a linha de graus de liberdade:
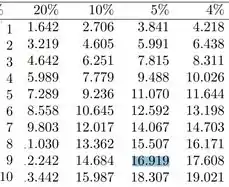
Portanto encontramos , então nossa RC assume a seguinte forma:
Ou seja, como , portanto ele está dentro da região crítica então devemos rejeitar a hipótese nula.
Por último, o exercício pede o nível descritivo, se você se lembrar ele nada mais é do que a chance de obtermos um valor tão mais extremo quanto o observado; em outras palavras:
Buscando por esse valor na tabela, novamente na linha de 9 graus de liberdade:
Perceba que 23,45 está ali no meiozinho daqueles valores destacados; isso significa que não bastasse todo o esforço até chegar aqui, vamos ter que fazer uma interpolação.
Mas calma que é rapidinho, olha só:
Só isolar :
Sendo esse o nosso nível descritivo.
Resposta
- .
- Existem evidências de que as variáveis sejam dependentes.