Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 35
Investiga-se, para um certo produto, a fidelidade (alta, média e baixa) de seus consumidores. em uma amostra de 200 homens e 200 mulheres, foram classificados como tendo alto grau de fidelidade de 120 homens e 80 mulheres, enquanto com grau médio, 50 mulheres e 50 homens. Os dados fornecem evidências de possíveis diferenças de grau de fidelidade entre os sexos?? Indique o teste realizado.
Passo 1
Olá, a gente veio fazendo em vários exercícios o teste de independência entre duas variáveis só que dessa vez ele não cabe aqui; você consegue identificar o porquê?
É bem simples ó... antes a gente analisava duas variáveis quantitativas, por exemplo renda e número de filhos, salário e grau de escolaridade, etc...
Só que agora a gente não tem duas variáveis, a gente tem uma única:
E temos duas subpopulações, homens e mulheres.
Portanto, o teste a ser realizado aqui é o que chamamos de “Teste de Homogeneidade”.
Mas não se preocupe (só se lamente), porque é a mesma fucking coisa que o teste de independência.
Passo 2
Perceba as semelhanças... aqui também iremos usar a aproximação pela distribuição Qui-quadrado:
Denovo, será os valores observados em cada célula, com linhas e colunas.
Aquele continua sendo o valor esperado em cada célula.
Viu como é quase igual.... quase.
Porque agora vamos obter esses valores esperado da seguinte forma:
Essa mudança se deve ao fato de que em cada linha teremos uma subpopulação; então no final das contas não muda quase nada.
O teste de hipótese a ser realizado agora é:
Contra:
Eii Cara peraí!! O exercício não deu p**** de tabela nenhuma!
Não mesmo.... mas ele deu tudo no texto... repara só:
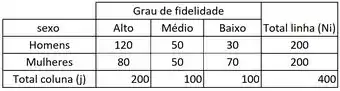
Percebeu? Sempre colocando as subpopulações nas linhas. Agora bora buscar os valores que eram esperados.
Passo 3
Bora.
Pegou o “taime”? Fazendo isso até:
Vou colocar os valores obtidos em outra tabelinha:
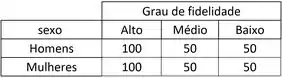
Agora, antes de realizar o teste qui-quadrado vamos montar a região crítica:
Como o enunciado nos dá , precisamos buscar um valor tal que:
Para achar esse garoto, vamos olhar na coluna de 2% e na linha de graus de liberdade.
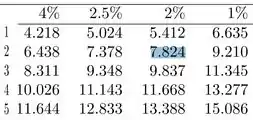
Ou seja, a nossa RC fica assim:
Agora, finalmente podemos realizar o teste:
E ai chegamos em:
Nitidamente, pertence à região crítica; então devemos rejeitar
Resposta
Concluimos que existem evidencias de que o grau de fidelidade seja diferente para homens e mulheres.