Quatro grupos de pacientes com úlcera duodenal foram submetidos a diferentes cirurgias caracterizadas pela porcentagem de tecido gástrico removido. A tabela apresentada a seguir contém dados referentes à classificação dos pacientes quanto à severidade de uma sequela indesejável da cirurgia.

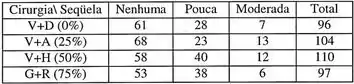
Verificar se existe associação entre a porcentagem de tecido gástrico removido e a severidade da sequela. Utilize o nível descritivo.

Vamos á isso então:

E assim até:

Vou botar tudo dentro de uma nova tabelinha só com esses valores esperados:

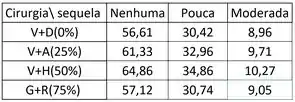
Tamo de acordo? Da um boa conferida aí; sempre tomando muito cuidado com as aproximações, pois a soma total das células da tabelinha acima tem que ser o mais próxima possível do valor total de 407. Blz?

Agora, podemos finalmente usar a aproximação pela Qui-quadrado:

Agora, para concluir o teste o enunciado pede para utilizar o nível descritivo, se você se recordar esse tal nível nada mais é do que a chance de obtermos um valor mais extremo do que o que acabamos de obter; em outras palavras:

Pegou a ideia? Então vamos precisar buscar esse valor na tabela de distribuição qui-quadrado, olhando na linha de graus de liberdade; lembrando que temos 4 linhas e 3 colunas na tabela.

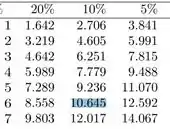
Ou seja, obtemos:

Sim, vamos aproximar porque não somos obrigados.

Agora, sabemos que provavelmente a hipótese nula será falsa para pequenos valores do nível descritivo; ai sempre vem aquela pergunta...

“Mas pequeno quanto?”

Então, aí depende sempre do nível de significância escolhido; olha bem... dessa vez tamos falando do nível de SIGNIFICÂNCIA... é aquele que na maioria das vezes os exercícios dão.

Lembrou? A gente usa eles como comparação; vamos refutar quando:

E aceitamos quando:

Nesse exercício não temos nem sinal de ...

Mas calma, se levarmos em consideração que na imensa maioria das vezes usamos um ou até menor do que isso, então um nível descritivo de é muita coisa não acha??

Portanto, vamos concluir que muito provavelmente a hipótese nula é verdadeira.