Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 31
Usando os dados abaixo, verifique descritivamente se existe dependência entre o número de filhos e o rendimento familiar (em reais). Em seguida, teste tal fato considerando um nível de significância de . (Não esqueça de formular as hipóteses).
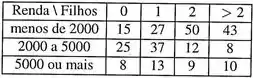
Passo 1
Dessa vez o teste a ser realizado é chamado de Teste de independência, por motivos óbvios; queremos testar se duas variáveis são ou não independentes; sendo elas:
E
Ou seja, teremos as seguinte teses:
Para isso, vamos usar mais uma vez a aproximação pela distribuição Qui-quadrado:
Onde e representam as linhas e colunas respectivamente com graus de liberdade e é exatamente o valor dado em cada célula. Chatinho né? Vamos devagar.
O representa um valor esperado para cada CÉLULA, ou seja:
E assim por diante, fazendo um arranjo das linhas e colunas.
Passo 2
Bora fazer isso então:
E assim por diante até:
Vou colocar todos os valores esperados numa tabelinha:
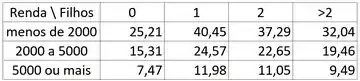
Certo, agora o próximo passo, é estabelecer uma região crítica utilizando a distribuição Qui-quadrado.
Passo 3
Vamos a isso então:
O enunciado nos forneceu , então vamos buscar na tabela um valor tal que:
Para tanto, basta irmos na coluna de 1% e na linha de:
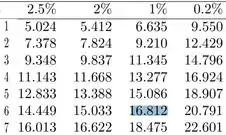
Portanto nossa Rc será da seguinte forma:
Agora, só nos resta realizar o teste:
Portanto, então devemos rejeitar
Resposta
Concluimos que existem evidencias de que a renda familiar seja dependente do número de filhos.