Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 14.Problemas - Ex. 13
Investigando a “fidelidade” de consumidores de um produto, obteve-se uma amostra de
homens e mulheres. Foram classificados como tendo alto grau de fidelidade
homens e mulheres. Os dados fornecem evidência de possíveis diferenças de grau de
fidelidade entre sexos?
Passo 1
Com base nos dados do exercício, vamos construir tabelas para a frequência observada e para frequência esperada :
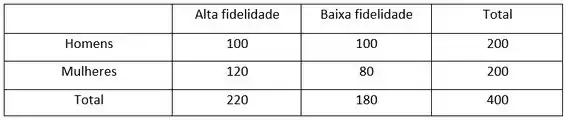
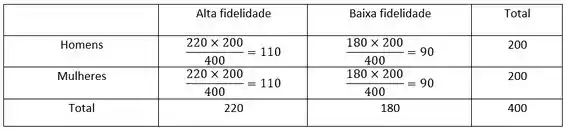
Agora, vamos construir uma tabela para a estatística:
Passo 2
Vamos calcular a estatística do teste:
O valor crítico do teste é .
Como , rejeitamos a hipótese de nulidade.
Resposta
Assim, como rejeitamos a hipótese de nulidade, concluímos que há evidências de que o grau de fidelidade ao produto depende do sexo.
Exercícios de Livros Relacionados
Usando os dados abaixo, verifique descritivamente se existe dependência entre o número de filhos e o rendimento familiar (em reais). Em seguida, teste tal fato considerando um nível de significância d
Em uma escola de ensino médio, o desempenho dos alunos em matemática e física foi observado (ver tabela a seguir) para testar se existe dependência entre as duas disciplinas.Calcule o nível descritíve
Acredita-se que o empenho de estudantes universitários muda no decorrer do curso. Para investigar essa afirmação, decidiu-se estudar a relação entre o ano de curso e aprovação em disciplinas. Os pesqu
Investiga-se, para um certo produto, a fidelidade (alta, média e baixa) de seus consumidores. em uma amostra de 200 homens e 200 mulheres, foram classificados como tendo alto grau de fidelidade de 120
Quatro grupos de pacientes com úlcera duodenal foram submetidos a diferentes cirurgias caracterizadas pela porcentagem de tecido gástrico removido. A tabela apresentada a seguir contém dados referente