Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 38
Consulte os dados sobre x = taxa de liberação e y = taxa de emissão de NOX fornecidos no Exercício 19. a. O modelo de regressão linear simples especifica uma relação útil entre as duas taxas? Use o procedimento de teste apropriado para obter informações sobre o valor P e, em seguida, tire uma conclusão usando o nível de significância 0,01. b. Calcule um IC de 95% para a mudança esperada na taxa de emissão associada com um aumento de 10 MBtu/h–pés2 na taxa de liberação.
Passo 1
- Do Exercício 23, que também se refere ao Exercício 19
- Um intervalo de confiança de para a inclinação na linha do modelo de regressão linear simples é
Então
E
Desta forma
Então o . Por conta do valor p ser menor que 0.01
é rejeitada no nível 0,01 a favor da conclusão de que o modelo é útil
Passo 2
Usando isso, o intervalo de confiança é
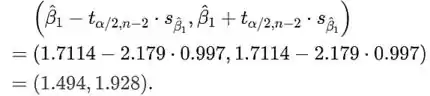
No entanto, a confiança do intervalo de interesse é para o parâmetro 10
Resposta
- Modelo é útil
Exercícios de Livros Relacionados
Em relação ao Exercício 12.9, encontre a estimativa de(a) O b 2 2 ,(b) C o v b 1 , b 4 .
O departamento de pessoal de uma indústriausou 12 indivíduos em um estudo para determinar a relação entre o índice de desempenho no trabalho (y) e osresultados de quatro testes. Os dados são os seguin
Um estudo foi conduzido para determinar se o pesode um animal pode ser previsto depois de um períodocom base no seu peso inicial e na quantidade de ração que ele comeu. Os seguintes dados, em quilogra
Usando os dados do Exercício 12.2 e a estimativade (T2 do Exercício 12.17, calcule o intervalo de confiança de 95% para a resposta predita e para a respostamédia quando x} = 900 e x ,= 1,00
Um experimento foi conduzido para estudar o tamanho das lulas comidas por tubarões e atuns. As variáveis regressoras são as características do bico ou boca dalula. As variáveis regressoras e as respo